Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Marín, J
Romaguera, S
and
Tirado, P
2011.
"Equation missing" -Functions on Quasimetric Spaces and Fixed Points for Multivalued Maps.
Fixed Point Theory and Applications,
Vol. 2011,
Issue. 1,
Marín, Josefa
Romaguera, Salvador
and
Tirado, Pedro
2011.
Weakly contractive multivalued maps and w-distances on complete quasi-metric spaces.
Fixed Point Theory and Applications,
Vol. 2011,
Issue. 1,
Pourmahdian, Massoud
and
Ali-Akbari, Mahdi
2011.
Computational Models of Certain Hyperspaces of Quasi-metric Spaces.
Logical Methods in Computer Science,
Vol. Volume 7, Issue 4,
Issue. ,
Romaguera, S.
Tirado, P.
and
Valero, O.
2012.
Complete partial metric spaces have partially metrizable computational models.
International Journal of Computer Mathematics,
Vol. 89,
Issue. 3,
p.
284.
Kemajou, Elisabeth
Künzi, Hans-Peter A.
and
Olela Otafudu, Olivier
2012.
The Isbell-hull of a di-space.
Topology and its Applications,
Vol. 159,
Issue. 9,
p.
2463.
Künzi, Hans-Peter A.
and
Olela Otafudu, Olivier
2012.
q-Hyperconvexity in Quasipseudometric Spaces and Fixed Point Theorems.
Journal of Function Spaces and Applications,
Vol. 2012,
Issue. ,
p.
1.
Alghamdi, Maryam A
Shahzad, Naseer
and
Valero, Oscar
2012.
On fixed point theory in partial metric spaces.
Fixed Point Theory and Applications,
Vol. 2012,
Issue. 1,
Alghamdi, Maryam A
Shahzad, Naseer
and
Valero, Oscar
2013.
Fixed point theorems in generalized metric spaces with applications to computer science.
Fixed Point Theory and Applications,
Vol. 2013,
Issue. 1,
Shahzad, N.
and
Valero, O.
2013.
On 0-Complete Partial Metric Spaces and Quantitative Fixed Point Techniques in Denotational Semantics.
Abstract and Applied Analysis,
Vol. 2013,
Issue. ,
p.
1.
Tao, Yuanye
Lai, Hongliang
and
Zhang, Dexue
2014.
Quantale-valued preorders: Globalization and cocompleteness.
Fuzzy Sets and Systems,
Vol. 256,
Issue. ,
p.
236.
Ricarte, Luis A.
and
Romaguera, Salvador
2014.
A domain-theoretic approach to fuzzy metric spaces.
Topology and its Applications,
Vol. 163,
Issue. ,
p.
149.
Romaguera, S.
Sánchez-Granero, M.A.
and
Sanchis, M.
2014.
On the construction of domains of formal balls for uniform spaces.
Topology and its Applications,
Vol. 168,
Issue. ,
p.
125.
Romaguera, Salvador
and
Tirado, Pedro
2015.
A characterization of Smyth complete quasi-metric spaces via Caristi’s fixed point theorem.
Fixed Point Theory and Applications,
Vol. 2015,
Issue. 1,
Romaguera, S.
Schellekens, M.P.
Tirado, P.
and
Valero, O.
2016.
On the domain of formal balls of the Sorgenfrey quasi-metric space.
Topology and its Applications,
Vol. 203,
Issue. ,
p.
177.
Mardones-Pérez, I.
and
de Prada Vicente, M.A.
2016.
An application of a representation theorem for fuzzy metrics to domain theory.
Fuzzy Sets and Systems,
Vol. 300,
Issue. ,
p.
72.
Gao, You
and
Zhou, Xiangnan
2017.
The Relationships Between KM-fuzzy Quasi-metric Spaces and the Associated Posets of Formal Balls.
Electronic Notes in Theoretical Computer Science,
Vol. 333,
Issue. ,
p.
17.
Ng, Kok Min
and
Ho, Weng Kin
2017.
Yoneda Completion via a DCPO Completion of its Poset of Formal Balls.
Electronic Notes in Theoretical Computer Science,
Vol. 333,
Issue. ,
p.
103.
de Brecht, Matthew
Goubault-Larrecq, Jean
Jia, Xiaodong
and
Lyu, Zhenchao
2019.
Domain-complete and LCS-complete Spaces.
Electronic Notes in Theoretical Computer Science,
Vol. 345,
Issue. ,
p.
3.
Ng, Kok Min
and
Ho, Weng Kin
2019.
Quasi-continuous Yoneda Complete Quasi-Metric Space.
Electronic Notes in Theoretical Computer Science,
Vol. 345,
Issue. ,
p.
185.
Cobzaş, S.
2020.
Fixed Points and Completeness in Metric and Generalized Metric Spaces.
Journal of Mathematical Sciences,
Vol. 250,
Issue. 3,
p.
475.
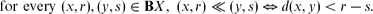 From this characterisation, we then deduce that a quasi-metric space (X, d) is Smyth-complete if and only if BX is a dcpo satisfying condition (*). We also give characterisations in terms of formal balls for sequentially Yoneda complete quasi-metric spaces and for Yoneda complete T1 quasi-metric spaces. Finally, we discuss several properties of the Heckmann quasi-metric on the formal balls of any quasi-metric space.
From this characterisation, we then deduce that a quasi-metric space (X, d) is Smyth-complete if and only if BX is a dcpo satisfying condition (*). We also give characterisations in terms of formal balls for sequentially Yoneda complete quasi-metric spaces and for Yoneda complete T1 quasi-metric spaces. Finally, we discuss several properties of the Heckmann quasi-metric on the formal balls of any quasi-metric space.



