Article contents
Air cushioning and bubble entrapment in three-dimensional droplet impacts
Published online by Cambridge University Press: 13 April 2010
Abstract
Droplet deformation by air cushioning prior to impact is considered. A model is presented coupling the free-surface deformation of a droplet with the pressure field in the narrow air layer generated as a droplet approaches an impact. The model is based upon the density and viscosity in the air being small compared with those in the liquid. Additionally, the Reynolds number, defined using the droplet radius ℛ and approach velocity 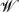 l, is such that lubrication forces dominate in the air layer. In the absence of significant surface tension or compressibility effects, these assumptions lead to coupled nonlinear integro-differential equations describing the evolution of a droplet free surface approaching a solid wall through air, with or without topography.
l, is such that lubrication forces dominate in the air layer. In the absence of significant surface tension or compressibility effects, these assumptions lead to coupled nonlinear integro-differential equations describing the evolution of a droplet free surface approaching a solid wall through air, with or without topography.
The problem is studied numerically with a boundary-element method in the inviscid droplet coupled with a finite-difference method in the lubricating air. In normal impacts, air cushioning will be shown to deflect the free surface upwards, delaying the moment of touchdown and trapping a bubble. The volume of the bubble is found to be (μg4/3ℛ5/3/ρl4/3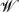 l4/3)
l4/3)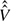 , where μg is the gas viscosity and ρl is the liquid density and the numerically computed pre-factor
, where μg is the gas viscosity and ρl is the liquid density and the numerically computed pre-factor 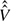 = 94.48. Bubble volumes predicted by this relationship are shown to be in good agreement with experimental observations. In oblique impact or impact with a moving surface with sufficient horizontal motion a bubble is not trapped beneath the approaching droplet. In this case, the region of touchdown is initially crescent shaped with air effects accelerating the moment of touchdown.
= 94.48. Bubble volumes predicted by this relationship are shown to be in good agreement with experimental observations. In oblique impact or impact with a moving surface with sufficient horizontal motion a bubble is not trapped beneath the approaching droplet. In this case, the region of touchdown is initially crescent shaped with air effects accelerating the moment of touchdown.
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2010
References
REFERENCES
- 116
- Cited by




