Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Revalski, Julian Petrov
1992.
An equivalence relation between optimization problems connected with the well-posedness.
Journal of Mathematical Analysis and Applications,
Vol. 168,
Issue. 2,
p.
469.
Bednarczuk, Ewa
and
Penot, Jean-Paul
1992.
Metrically well-set minimization problems.
Applied Mathematics & Optimization,
Vol. 26,
Issue. 3,
p.
273.
Kenderov, P. S.
and
Revalski, J. P.
1993.
The Banach-Mazur game and generic existence of solutions to optimization problems.
Proceedings of the American Mathematical Society,
Vol. 118,
Issue. 3,
p.
911.
Revalski, J. P.
and
Zhivkov, N. V.
1993.
Well-posed constrained optimization problems in metric spaces.
Journal of Optimization Theory and Applications,
Vol. 76,
Issue. 1,
p.
145.
Debs, Gabriel
and
Raymond, Jean Saint
1994.
Topological games and optimization problems.
Mathematika,
Vol. 41,
Issue. 1,
p.
117.
Patrone, F.
1995.
Recent Developments in Well-Posed Variational Problems.
p.
211.
Revalski, J. P.
1995.
Recent Developments in Well-Posed Variational Problems.
p.
229.
Kenderov, P. S.
and
Revalski, J. P.
1995.
Recent Developments in Well-Posed Variational Problems.
p.
117.
Čoban, M. M.
Kenderov, P. S.
and
Revalski, J. P.
1995.
Topological spaces related to the Banach-Mazur game and the generic well-posedness of optimization problems.
Set-Valued Analysis,
Vol. 3,
Issue. 3,
p.
263.
Kenderov, P.S.
and
Lucchetti, R.E.
1996.
Generic well posedness of supinf problems.
Bulletin of the Australian Mathematical Society,
Vol. 54,
Issue. 1,
p.
5.
Deville, Robert
and
Revalski, Julian
1999.
Porosity of ill-posed problems.
Proceedings of the American Mathematical Society,
Vol. 128,
Issue. 4,
p.
1117.
Bachir, Mohammed
2001.
A Non-Convex Analogue to Fenchel Duality.
Journal of Functional Analysis,
Vol. 181,
Issue. 2,
p.
300.
Kenderov, P.S.
Kortezov, I.S.
and
Moors, W.B.
2001.
Continuity points of quasi-continuous mappings.
Topology and its Applications,
Vol. 109,
Issue. 3,
p.
321.
Ioffe, A. D.
Lucchetti, R. E.
and
Revalski, J. P.
2002.
A Variational Principle for Problems with Functional Constraints.
SIAM Journal on Optimization,
Vol. 12,
Issue. 2,
p.
461.
Lin, Zhi
and
Yu, Jian
2004.
On well-posedness of the multiobjective generalized game.
Applied Mathematics-A Journal of Chinese Universities,
Vol. 19,
Issue. 3,
p.
327.
Ioffe, A.
and
Lucchetti, R. E.
2005.
Typical convex program is very well posed.
Mathematical Programming,
Vol. 104,
Issue. 2-3,
p.
483.
Xiang, Shuwen
Jia, Wensheng
He, Jihao
Xia, Shunyou
and
Chen, Zhiyou
2012.
Some results concerning the generic continuity of set-valued mappings.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 75,
Issue. 8,
p.
3591.
Choban, Mitrofan M.
Kenderov, Petar S.
and
Revalski, Julian P.
2012.
Variational principles and topological games.
Topology and its Applications,
Vol. 159,
Issue. 17,
p.
3550.
Kenderov, P. S.
and
Revalski, J. P.
2012.
Variational principles in non-metrizable spaces.
TOP,
Vol. 20,
Issue. 2,
p.
467.
Penot, Jean-Paul
2013.
Calculus Without Derivatives.
Vol. 266,
Issue. ,
p.
117.
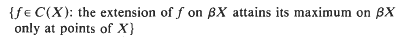
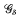 -subset of C(X). These are just the spaces X which contain a dense Čech complete subspace. We call such spaces almost Čech complete. We also prove that X contains a dense completely metrizable subspace, if, and only if, C(X) contains a dense
-subset of C(X). These are just the spaces X which contain a dense Čech complete subspace. We call such spaces almost Čech complete. We also prove that X contains a dense completely metrizable subspace, if, and only if, C(X) contains a dense 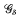 -subset of functions which determine Tykhonov well-posed optimization problems over X. For a compact Hausdorff topological space X the latter result was proved by Čoban and Kenderov [CK1.CK2]. Relations between the well-posedness and Gâteaux and Fréchet differentiability of convex functionals in C(X) are investigated. In particular it is shown that the sup-norm in C(X) is Frechet differentiable at the points of a dense
-subset of functions which determine Tykhonov well-posed optimization problems over X. For a compact Hausdorff topological space X the latter result was proved by Čoban and Kenderov [CK1.CK2]. Relations between the well-posedness and Gâteaux and Fréchet differentiability of convex functionals in C(X) are investigated. In particular it is shown that the sup-norm in C(X) is Frechet differentiable at the points of a dense 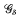 -subset of C(X), if, and only if, the set of isolated points of X is dense in X. Conditions and examples are given when the set of points of Gateaux differentiability of the sup-norm in C(X) is a dense and Baire subspace of C(X) but does not contain a dense
-subset of C(X), if, and only if, the set of isolated points of X is dense in X. Conditions and examples are given when the set of points of Gateaux differentiability of the sup-norm in C(X) is a dense and Baire subspace of C(X) but does not contain a dense  -subset of C(X).
-subset of C(X).



