Article contents
Minkowski sums of projections of convex bodies
Published online by Cambridge University Press: 26 February 2010
Abstract
If K is a convex body in 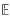 d and 1≤k≤d − 1, we define Pk(K) to be the Minkowski sum or Minkowski average of all the projections of K onto k-dimensional subspaces of
d and 1≤k≤d − 1, we define Pk(K) to be the Minkowski sum or Minkowski average of all the projections of K onto k-dimensional subspaces of 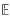 d. The operator Pd − 1, was first introduced by Schneider, who showed that, if Pd − 1(K) = cK, then K is a ball. More recently, Spriestersbach showed that, if Pd − 1(K) = cK then K = M. In addition, she gave stability versions of this result and Schneider's. We will describe further injectivity results for the operators Pk. In particular, we will show that Pk is injective if k≤d/2 and that P2 is injective in all dimensions except d = 14, where it is not injective.
d. The operator Pd − 1, was first introduced by Schneider, who showed that, if Pd − 1(K) = cK, then K is a ball. More recently, Spriestersbach showed that, if Pd − 1(K) = cK then K = M. In addition, she gave stability versions of this result and Schneider's. We will describe further injectivity results for the operators Pk. In particular, we will show that Pk is injective if k≤d/2 and that P2 is injective in all dimensions except d = 14, where it is not injective.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1998
References
- 6
- Cited by




