Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Lukes, Richard
Scheidler, Renate
and
Williams, Hugh
1997.
Further tabulation of the Erdös-Selfridge function.
Mathematics of Computation,
Vol. 66,
Issue. 220,
p.
1709.
Konyagin, S. V.
1999.
Estimates of the least prime factor of a binomial coefficient.
Mathematika,
Vol. 46,
Issue. 1,
p.
41.
Ruzsa, Imre Z.
1999.
Erdős and the Integers.
Journal of Number Theory,
Vol. 79,
Issue. 1,
p.
115.
Granville, Andrew
1999.
On the scarcity of powerful binomial coefficients.
Mathematika,
Vol. 46,
Issue. 2,
p.
397.
Cutter, Pamela
2001.
Finding prime pairs with particular gaps.
Mathematics of Computation,
Vol. 70,
Issue. 236,
p.
1737.
Stănică, Pantelimon
2003.
pq-Catalan numbers and squarefree binomial coefficients.
Journal of Number Theory,
Vol. 100,
Issue. 2,
p.
203.
Cheng, Yuanyou F.
and
Graham, Sidney W.
2004.
Explicit Estimates for the Riemann Zeta Function.
Rocky Mountain Journal of Mathematics,
Vol. 34,
Issue. 4,
Moshe, Yossi
2004.
On a problem of Granville and Zhu Regarding Pascal's triangle.
Mathematika,
Vol. 51,
Issue. 1-2,
p.
63.
Chen, William Y.C.
and
Hou, Qing-Hu
2006.
Factors of the Gaussian coefficients.
Discrete Mathematics,
Vol. 306,
Issue. 13,
p.
1446.
SHEVELEV, VLADIMIR
2007.
ON DIVISIBILITY OF ${\fontsize{9}{11}\selectfont\Big(\!\!\begin{array}{c}n-i-1\\[2pt]i-1\end{array}\!\!\Big)}$ by i.
International Journal of Number Theory,
Vol. 03,
Issue. 01,
p.
119.
Luca, Florian
and
Varona, Juan Luis
2009.
Multiperfect numbers on lines of the Pascal triangle.
Journal of Number Theory,
Vol. 129,
Issue. 5,
p.
1136.
Brüdern, Jörg
and
Daemen, Dirk
2009.
Imperfect Mimesis of Weyl Sums.
International Mathematics Research Notices,
Vol. 2009,
Issue. 16,
p.
3112.
Narkiewicz, Władysław
2012.
Rational Number Theory in the 20th Century.
p.
195.
Bordellès, Olivier
2012.
Arithmetic Tales.
p.
297.
Ramaré, Olivier
2013.
Some elementary explicit bounds for two mollifications of the Moebius function.
Functiones et Approximatio Commentarii Mathematici,
Vol. 49,
Issue. 2,
Fedorov, G. V.
2013.
Number of divisors of the central binomial coefficient.
Moscow University Mathematics Bulletin,
Vol. 68,
Issue. 4,
p.
194.
Luca, Florian
2013.
On the Diophantine equation f(n)=u!+v!,.
Glasnik Matematicki,
Vol. 48,
Issue. 1,
p.
31.
TRUDGIAN, TIMOTHY
2014.
A NEW UPPER BOUND FOR .
Bulletin of the Australian Mathematical Society,
Vol. 89,
Issue. 2,
p.
259.
Green, Ben
and
Harper, Adam J
2014.
Inverse questions for the large sieve.
Geometric and Functional Analysis,
Vol. 24,
Issue. 4,
p.
1167.
Filaseta, M.
Graham, S.
and
Trifonov, O.
2015.
Starting with gaps between k-free numbers.
International Journal of Number Theory,
Vol. 11,
Issue. 05,
p.
1411.
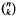 must be highly composite in that it contains many prime factors and often to high powers. It is therefore of interest to enquire as to how infrequently
must be highly composite in that it contains many prime factors and often to high powers. It is therefore of interest to enquire as to how infrequently 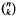 is squarefree. One well-known conjecture, due to Erdős, is that
is squarefree. One well-known conjecture, due to Erdős, is that 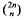 is not squarefree once n > 4. Sarközy [Sz] proved this for sufficiently large n but here we return to and solve the original question.
is not squarefree once n > 4. Sarközy [Sz] proved this for sufficiently large n but here we return to and solve the original question.



