Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chen, Jun-Fan
2012.
A Note on the Growth of Meromorphic Functions with a Radially Distributed Value.
Abstract and Applied Analysis,
Vol. 2012,
Issue. ,
p.
1.
Chen, Wei
Zhang, Yingying
Zeng, Jiwen
and
Tian, Honggen
2012.
Normal Criterion Concerning Shared Values.
Journal of Applied Mathematics,
Vol. 2012,
Issue. ,
p.
1.
Li, Yuntong
2012.
Normal Families of Zero-Free Meromorphic Functions.
Abstract and Applied Analysis,
Vol. 2012,
Issue. ,
p.
1.
LEI, Chunlin
FANG, Mingliang
and
ZENG, Cuiping
2013.
Some Normality Criteria of Meromorphic Functions.
Acta Mathematica Scientia,
Vol. 33,
Issue. 6,
p.
1667.
Battaglia, Erika
and
Bonfiglioli, Andrea
2014.
Normal families of functions for subelliptic operators and the theorems of Montel and Koebe.
Journal of Mathematical Analysis and Applications,
Vol. 409,
Issue. 1,
p.
1.
Qi, Jianming
Zhang, Guowei
and
Yuan, Wenjun
2014.
Radically distributed value and normal families of meromorphic functions.
Frontiers of Mathematics in China,
Vol. 9,
Issue. 2,
p.
355.
LIAO, LIANG-WEN
and
YE, ZHUAN
2014.
ON SOLUTIONS TO NONHOMOGENEOUS ALGEBRAIC DIFFERENTIAL EQUATIONS AND THEIR APPLICATION.
Journal of the Australian Mathematical Society,
Vol. 97,
Issue. 3,
p.
391.
WANG, YOU-MING
2015.
The Normality of Meromorphic Functions with Multiple Zeros and Poles Concerning Sharing Values.
Kyungpook mathematical journal,
Vol. 55,
Issue. 3,
p.
641.
Kumar, Sanjay
and
Rani, Poonam
2020.
Normality criteria for families of meromorphic functions.
Indian Journal of Pure and Applied Mathematics,
Vol. 51,
Issue. 2,
p.
579.




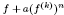 assumes each value
assumes each value 