Article contents
On odd perfect numbers (II), multiperfect numbers and quasiperfect numbers
Published online by Cambridge University Press: 09 April 2009
Extract
Let N be a positive integer. This paper is concerned with obtaining bounds for 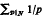 (p prime), when N is an odd perfect number, a multiperfect number, or a quasiperfect number, under assumptions on the existence of such numbers (where none is known) and whether 3 and 5 are divisors. We argue that our new lower bounds in the case of odd perfect numbers are not likely to be significantly improved further. Triperfect numbers are investigated in some detail, and it is shown that an odd triperfect number must have at least nine distinct prime factors.
(p prime), when N is an odd perfect number, a multiperfect number, or a quasiperfect number, under assumptions on the existence of such numbers (where none is known) and whether 3 and 5 are divisors. We argue that our new lower bounds in the case of odd perfect numbers are not likely to be significantly improved further. Triperfect numbers are investigated in some detail, and it is shown that an odd triperfect number must have at least nine distinct prime factors.
1980 Mathematics subject classification (Amer. Math. Soc.): 10 A 20.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1980
References
- 10
- Cited by




