Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Szekeres, G.
1974.
Combinatorial Mathematics.
Vol. 403,
Issue. ,
p.
125.
Isaacs, Rufus
1975.
Infinite Families of Nontrivial Trivalent Graphs Which are not Tait Colorable.
The American Mathematical Monthly,
Vol. 82,
Issue. 3,
p.
221.
Szekeres, G.
1975.
Combinatorial Mathematics III.
Vol. 452,
Issue. ,
p.
227.
Giles, J. R.
and
Wallis, Jennifer Seberry
1976.
George Szekeres.
Journal of the Australian Mathematical Society,
Vol. 21,
Issue. 4,
p.
385.
Tutte, W. T.
1978.
Colouring problems.
The Mathematical Intelligencer,
Vol. 1,
Issue. 2,
p.
72.
Fiorini, S.
1978.
A bibliographic survey of edge‐colorings.
Journal of Graph Theory,
Vol. 2,
Issue. 2,
p.
93.
Preissmann, M.
1980.
Even polyhedral decompositions of cubic graphs.
Discrete Mathematics,
Vol. 32,
Issue. 3,
p.
331.
Goldberg, Mark K
1981.
Construction of class 2 graphs with maximum vertex degree 3.
Journal of Combinatorial Theory, Series B,
Vol. 31,
Issue. 3,
p.
282.
Seymour, P.D
1981.
Even circuits in planar graphs.
Journal of Combinatorial Theory, Series B,
Vol. 31,
Issue. 3,
p.
327.
Goddyn, Luis
1985.
Annals of Discrete Mathematics (27): Cycles in Graphs.
Vol. 115,
Issue. ,
p.
13.
Jaeger, Francois
1985.
Annals of Discrete Mathematics (27): Cycles in Graphs.
Vol. 115,
Issue. ,
p.
1.
Goddyn, Luis A
1989.
Cycle double covers of graphs with Hamilton paths.
Journal of Combinatorial Theory, Series B,
Vol. 46,
Issue. 2,
p.
253.
Catlin, Paul A.
1989.
Double cycle covers and the petersen graph.
Journal of Graph Theory,
Vol. 13,
Issue. 4,
p.
465.
Bondy, J. A.
1990.
Cycles and Rays.
p.
21.
Bondy, J. A.
1990.
Perfect path double covers of graphs.
Journal of Graph Theory,
Vol. 14,
Issue. 2,
p.
259.
Catlin, P. A.
1990.
Topics in Combinatorics and Graph Theory.
p.
185.
Bondy, J. A.
and
Fan, Genghua
1991.
Cycles in weighted graphs.
Combinatorica,
Vol. 11,
Issue. 3,
p.
191.
Seyffarth, Karen
1992.
Hajós' conjecture and small cycle double covers of planar graphs.
Discrete Mathematics,
Vol. 101,
Issue. 1-3,
p.
291.
Catlin, Paul A.
1992.
Supereulerian graphs: A survey.
Journal of Graph Theory,
Vol. 16,
Issue. 2,
p.
177.
Fan, Genghua
1992.
Integer flows and cycle covers.
Journal of Combinatorial Theory, Series B,
Vol. 54,
Issue. 1,
p.
113.
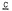 = {C1, C2, … Cm} with the property that every edge of G occurs exactly twice as an edge of some Ck. The decomposition is called even if every Ck is a simple circuit of even length. If G has a Tait colouring by three colours a, b, c then the (a, b), (b, c) and (c, a) circuits obviously form an even polyhedral decomposition. It is shown that the converse is also true: if G has an even polyhedral decomposition then it also has a Tait colouring. This permits an equivalent formulation of the four colour conjecture (and a much stronger conjecture of Branko Grünbaum) in terms of polyhedral decompositions alone.
= {C1, C2, … Cm} with the property that every edge of G occurs exactly twice as an edge of some Ck. The decomposition is called even if every Ck is a simple circuit of even length. If G has a Tait colouring by three colours a, b, c then the (a, b), (b, c) and (c, a) circuits obviously form an even polyhedral decomposition. It is shown that the converse is also true: if G has an even polyhedral decomposition then it also has a Tait colouring. This permits an equivalent formulation of the four colour conjecture (and a much stronger conjecture of Branko Grünbaum) in terms of polyhedral decompositions alone.



