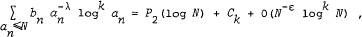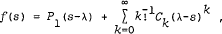Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Balakrishnan, U.
1987.
Laurent expansion of Dirichlet series-II.
Monatshefte f�r Mathematik,
Vol. 103,
Issue. 1,
p.
1.
Shirasaka, S.
2002.
On the Laurent coefficients of a class of Dirichlet series.
Results in Mathematics,
Vol. 42,
Issue. 1-2,
p.
128.
Wang, N.-L.
Agarwal, Praveen
and
Kanemitsu, S.
2020.
Limiting Values and Functional and Difference Equations.
Mathematics,
Vol. 8,
Issue. 3,
p.
407.




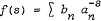 and its Laurent expansion at the abscissa of convergence, λ, say. When
and its Laurent expansion at the abscissa of convergence, λ, say. When