Article contents
Topological and order-topological orthomodular lattices
Published online by Cambridge University Press: 17 April 2009
Abstract
The necessary and sufficient conditions for atomic orthomodular lattices to have the MacNeille completion modular, or (o)-continuous or order topological, orthomodular lattices are proved. Moreover we show that if in an orthomodular lattice the (o)-convergence of filters is topological then the (o)-convergence of nets need not be topological. Finally we show that even in the case when the MacNeille completion 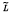 of an orthomodular lattice L is order-topological, then in general the (o)-convergence of nets in
of an orthomodular lattice L is order-topological, then in general the (o)-convergence of nets in 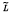 does not imply their (o)-convergence in L. (This disproves, also for the orthomodular and order-topological case, one statement in G.Birkhoff's book.)
does not imply their (o)-convergence in L. (This disproves, also for the orthomodular and order-topological case, one statement in G.Birkhoff's book.)
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 46 , Issue 3 , December 1992 , pp. 509 - 518
- Copyright
- Copyright © Australian Mathematical Society 1992
References
- 4
- Cited by




