Article contents
Interior regularity of the degenerate Monge-Ampère equation
Published online by Cambridge University Press: 17 April 2009
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
We study interior C1,1 regularity of generalised solutions of the Monge-Ampére equation det D2u = ψ, ψ ≥ 0, on a bounded convex domain Ω in ℝn with u = ϕ on ∂Ω. We prove in particular that u ∈ C1,1(Ω) if either i) ϕ = 0 and ψ1/(n − 1) ∈ C1,1 (Ω) or ii) Ω is C1,1 strongly convex, ϕ ∈ C1,1 (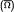 ), ψ1/(n − 1) ∈ C1,1(
), ψ1/(n − 1) ∈ C1,1(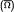 ) and ψ > 0 on U ∩ Ω, where U is a neighbourhood of ∂Ω. The main tool is an improvement of Pogorelov's well known C1,1 estimate so that it can be applied to the degenerate case.
) and ψ > 0 on U ∩ Ω, where U is a neighbourhood of ∂Ω. The main tool is an improvement of Pogorelov's well known C1,1 estimate so that it can be applied to the degenerate case.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 2003
References
[1]Aleksandrov, A.D., ‘Smoothness of a convex surface of bounded Gaussian curvature’, Dokl. Akad. Nauk SSSR 36 (1942), 195–199.Google Scholar
[2]Blocki, Z., ‘Smooth exhaustion functions in convex domains’, Proc. Amer. Math. Soc. 125 (1997), 477–484.CrossRefGoogle Scholar
[3]Blocki, Z., ‘Interior regularity of the complex Monge-Ampère equation in convex domains’, Duke Math. J. 105 (2000), 167–181.CrossRefGoogle Scholar
[4]Blocki, Z., ‘The C 1,1 regularity of the pluricomplex Green function’, Michigan Math. J. 47 (2000), 211–215.CrossRefGoogle Scholar
[5]Blocki, Z., ‘Regularity of the pluricomplex Green function with several poles’, Indiana Univ Math. J. 50 (2001), 335–351.CrossRefGoogle Scholar
[6]Caffarelli, L., Nirenberg, L. and Spruck, J., ‘The Dirichlet problem for nonlinear second order elliptic equations I: Monge-Ampère equation’, Comm. Pure Appl. Math. 37 (1984), 369–402.CrossRefGoogle Scholar
[7]Cheng, S.-Y. and Yau, S.-T., ‘Differential equations on Riemannian manifolds and their geometric applications’, Comm. Pure Appl. Math. 28 (1975), 333–354.CrossRefGoogle Scholar
[8]Cheng, S.-Y. and Yau, S.-T., ‘On the regularity of the Monge-Ampère equation det (∂2u/∂x i∂x j)= F(x, u)’, Comm. Pure Appl. Math. 30 (1977), 41–68.CrossRefGoogle Scholar
[9]Cheng, S.-Y. and Yau, S.-T., ‘The real Monge-Ampère equation and affine flat structures’, in Proc. Symp. Diff. Geom. Diff. Eq. (Beijing, 1980) 1, (Chern, S.S. and Wu, W.T., Editors) (Science Press, Beijing, 1982), pp. 339–370.Google Scholar
[10]Cheng, S.-Y. and Yau, S.-T., ‘On the existence of a complete Kähler metric on non-compact complex manifolds and the regularity of Fefferman's equation’, Comm. Pure Appl. Math. 33 (1980), 507–544.CrossRefGoogle Scholar
[11]Guan, B., ‘The Dirichlet problem for complex Monge-Ampère equations and regularity of the pluri-complex Green function’, Comm. Anal. Geom. 6 (1998), 687–703; Correction: Comm. Anal. Geom. 8 (2000), 213–218.CrossRefGoogle Scholar
[12]Guan, P., ‘C 2 priori estimates for degenerate Monge-Ampere equations’, Duke Math. J. 86 (1997), 323–346.CrossRefGoogle Scholar
[13]Guan, P., Trudinger, N.S. and Wang, X.-J., ‘On the Dirichlet problem for degenerate Mong-Ampère equations’, Acta Math. 182 (1999), 87–104.CrossRefGoogle Scholar
[14]Ivochkina, N.M., ‘Construction of a priori bounds for convex solutions of the Monge-Ampere equation by integral methods’, Ukrainian Math. J. 30 (1978), 32–38.CrossRefGoogle Scholar
[15]Krylov, N.V., ‘Boundedly inhomogeneous elliptic and parabolic equations in a domain’, (in Russian), Izv. Acad. Nauk SSSR Ser. Mat. 47 (1983), 75–108; English translation: Math. USSR-Izv. 22 (1984), 67–98.Google Scholar
[16]Pogorelov, A. V., ‘Soviet Math. Dokl.’, Dokl. Akad. Nauk SSSR 12 (1971), 1436–1440.Google Scholar
[17]Rauch, J. and Taylor, B.A., ‘The Dirichlet problem for the multidimensional Monge-Ampère equation’, Rocky Mountain Math. J. 7 (1977), 345–364.CrossRefGoogle Scholar
[18]Schulz, F., ‘A C 2 -estimate for solutions of complex Monge-Ampère equations’, J. Reine Angew. Math. 348 (1984), 88–93.Google Scholar
[19]Trudinger, N.S. and Urbas, J., ‘On second derivative eatimates for equations of Monge-Ampère type’, Bull. Austral. Math. Soc. 28 (1983), 321–334.Google Scholar
[20]Urbas, J., ‘Regularity of generalized solutions of the Monge-Ampère equation’, Math Z. 197 (1988), 365–393.CrossRefGoogle Scholar
[21]Wang, X.-J., ‘Some counterexamples to the regularity of Monge-Ampère equations’ Proc. Amer. Math. Soc. 123 (1995), 841–845.Google Scholar
- 6
- Cited by




