Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Banks, William D.
and
Shparlinski, Igor E.
2007.
Prime divisors in Beatty sequences.
Journal of Number Theory,
Vol. 123,
Issue. 2,
p.
413.
Shparlinski, Igor
2008.
Bilinear character sums over elliptic curves.
Finite Fields and Their Applications,
Vol. 14,
Issue. 1,
p.
132.
Technau, Marc
2020.
Modular hyperbolas and Beatty sequences.
Journal of Number Theory,
Vol. 208,
Issue. ,
p.
148.
Shparlinski, Igor E.
and
Technau, Marc
2020.
Kloosterman sums with twice-differentiable functions.
Functiones et Approximatio Commentarii Mathematici,
Vol. 63,
Issue. 1,
Jing, Mengyao
and
Liu, Huaning
2022.
Consecutive Quadratic Residues and Primitive Roots in the Sequences Formed by Twice-differentiable Functions.
Taiwanese Journal of Mathematics,
Vol. 26,
Issue. 3,
ÇAM ÇELİK, Şermin
2022.
k-Free numbers and integer parts of αp.
Communications Faculty Of Science University of Ankara Series A1Mathematics and Statistics,
Vol. 71,
Issue. 1,
p.
237.
Deraman, F.
Sapar, S. H.
Johari, M. A. M.
Ismail, Sh.
Yahya, Z.
and
Atan, K. A. Mohd
2022.
On cardinality of character sums with Beatty sequences associated with Fibonacci numbers.
Vol. 2465,
Issue. ,
p.
020005.
Jing, Mengyao
and
Liu, Huaning
2023.
KLOOSTERMAN SUMS WITH BEATTY SEQUENCES AND APPLICATION.
Rocky Mountain Journal of Mathematics,
Vol. 53,
Issue. 3,
Jing, Mengyao
and
Liu, Huaning
2023.
Consecutive quadratic residues in Beatty sequences.
International Journal of Number Theory,
Vol. 19,
Issue. 05,
p.
1167.
Jing, Mengyao
and
Liu, Huaning
2023.
Exponential sums with Piatetski-Shapiro sequences and their application to modular hyperbolas.
Journal of Number Theory,
Vol. 249,
Issue. ,
p.
400.
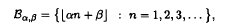 where α,β ∈ ℝ, and α is irrational. In particular, our bounds imply that for every fixed ε > 0, if p is sufficiently large and p½+ε ≤ N ≤ p, then among the first N elements of ℬα,β, there are N/2+o(N) quadratic non-residues modulo p. When more information is available about the Diophantine properties of α, then the error term o(N) admits a sharper estimate.
where α,β ∈ ℝ, and α is irrational. In particular, our bounds imply that for every fixed ε > 0, if p is sufficiently large and p½+ε ≤ N ≤ p, then among the first N elements of ℬα,β, there are N/2+o(N) quadratic non-residues modulo p. When more information is available about the Diophantine properties of α, then the error term o(N) admits a sharper estimate.



