Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chen, Imin
and
Siksek, Samir
2009.
Perfect powers expressible as sums of two cubes.
Journal of Algebra,
Vol. 322,
Issue. 3,
p.
638.




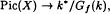 Where
Where

