Article contents
Measure convergent sequences in Lebesgue spaces and Fatou's lemma
Published online by Cambridge University Press: 17 April 2009
Abstract
Let (fn) be a sequence of positive P-integrable functions such that (∫ fndP)n converges. We prove that (fn) converges in measure to 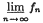 if and only if equality holds in the generalised Fatou's lemma. Let f∞ be an integrable function such that (∥fn − f∞∥1)n converges. We present in terms of the modulus of uniform integrability of (fn) necessary and sufficient conditions for (fn) to converge in measure to f∞.
if and only if equality holds in the generalised Fatou's lemma. Let f∞ be an integrable function such that (∥fn − f∞∥1)n converges. We present in terms of the modulus of uniform integrability of (fn) necessary and sufficient conditions for (fn) to converge in measure to f∞.
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 54 , Issue 2 , October 1996 , pp. 197 - 202
- Copyright
- Copyright © Australian Mathematical Society 1996
References
REFERENCES
- 1
- Cited by




