Article contents
Parameter rays in the space of exponential maps
Published online by Cambridge University Press: 01 April 2009
Abstract
We investigate the set I of parameters κ∈ℂ for which the singular orbit (0,eκ,…) of Eκ(z):=exp (z+κ) converges to 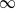 . These parameters are organized in curves in parameter space called parameter rays, together with endpoints of certain rays. Parameter rays are an important tool to understand the detailed structure of exponential parameter space. In this paper, we construct and investigate these parameter rays. Based on these results, a complete classification of the set I is given in the following paper [M. Förster, L. Rempe and D. Schleicher. Classification of escaping exponential maps. Proc. Amer. Math. Soc.136 (2008), 651–663].
. These parameters are organized in curves in parameter space called parameter rays, together with endpoints of certain rays. Parameter rays are an important tool to understand the detailed structure of exponential parameter space. In this paper, we construct and investigate these parameter rays. Based on these results, a complete classification of the set I is given in the following paper [M. Förster, L. Rempe and D. Schleicher. Classification of escaping exponential maps. Proc. Amer. Math. Soc.136 (2008), 651–663].
- Type
- Research Article
- Information
- Copyright
- Copyright © Cambridge University Press 2008
References
- 9
- Cited by




