Article contents
An Analytical Comparison of Variance and Semivariance Capital Market Theories
Published online by Cambridge University Press: 06 April 2009
Extract
Most research in modern portfolio theory and capital market theory is based on investor selection of portfolios that are efficient in the sense that they are not dominated by other portfolios in terms of their risk-expected return characteristics. The most widely used measure of portfolio risk is the variance about the mean of the exante distribution of portfolio returns. The theoretical framework from which this measure of risk is usually derived was initially suggested by Markowitz [12], and is by now well known. Although variance has the attention of most researchers, another measure, semivariance, had some early support from Markowitz himself, and from Quirk and Saposnik [17], Mao [10], and others. Semivariance as a measure of risk can be derived from the same theoretical framework as is variance; it requires only a slightly different utility function. The semivariance of returns of portfolio p below some point h is defined as
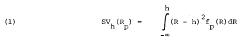
where fp (R) represents the probability density function of returns for portfolio p. Semivariance portfolio theory is enjoying something of a revival in the works of Porter [15, 16], Hogan and Warren [6] and Klemkosky [8], and semivariance capital market models have been developed by Hogan and Warren [7] and Greene [5].
- Type
- Research Article
- Information
- Copyright
- Copyright © School of Business Administration, University of Washington 1979
References
REFERENCES
- 42
- Cited by




