Hostname: page-component-8448b6f56d-xtgtn Total loading time: 0 Render date: 2024-04-15T18:59:41.944Z Has data issue: false hasContentIssue false
  • English
  • Français

Geometry of enstrophy and dissipation, grid resolution effects and proximity issues in turbulence

Published online by Cambridge University Press:  10 February 2009

IVÁN BERMEJO-MORENO ,
D. I. PULLIN  and
KIYOSI HORIUTI
IVÁN BERMEJO-MORENO*
Affiliation:
Graduate Aeronautical Laboratories, 205-45, California Institute of Technology, Pasadena, CA 91125, USA
D. I. PULLIN
Affiliation:
Graduate Aeronautical Laboratories, 205-45, California Institute of Technology, Pasadena, CA 91125, USA
KIYOSI HORIUTI
Affiliation:
Department of Mechano-Aerospace Engineering, Tokyo Institute of Technology, Tokyo 152-8552, Japan
*
†Email address for correspondence: ibermejo@caltech.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We perform a multi-scale non-local geometrical analysis of the structures extracted from the enstrophy and kinetic energy dissipation-rate, instantaneous fields of a numerical database of incompressible homogeneous isotropic turbulence decaying in time obtained by DNS in a periodic box. Three different resolutions are considered: 2563, 5123 and 10243 grid points, with kmax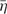 approximately 1, 2 and 4, respectively, the same initial conditions and Reλ ≈ 77. This allows a comparison of the geometry of the structures obtained for different resolutions. For the highest resolution, structures of enstrophy and dissipation evolve in a continuous distribution from blob-like and moderately stretched tube-like shapes at the large scales to highly stretched sheet-like structures at the small scales. The intermediate scales show a predominance of tube-like structures for both fields, much more pronounced for the enstrophy field. The dissipation field shows a tendency towards structures with lower curvedness than those of the enstrophy, for intermediate and small scales. The 2563 grid resolution case (kmax 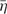≈ 1) was unable to detect the predominance of highly stretched sheet-like structures at the smaller scales in both fields. The same non-local methodology for the study of the geometry of structures, but without the multi-scale decomposition, is applied to two scalar fields used by existing local criteria for the eduction of tube- and sheet-like structures in turbulence, Q and [Aij]+, respectively, obtained from invariants of the velocity-gradient tensor and alike in the 10243 case. This adds the non-local geometrical characterization and classification to those local criteria, assessing their validity in educing particular geometries. Finally, we introduce a new methodology for the study of proximity issues among structures of different fields, based on geometrical considerations and non-local analysis, by taking into account the spatial extent of the structures. We apply it to the four fields previously studied. Tube-like structures of Q are predominantly surrounded by sheet-like structures of [Aij]+, which appear at closer distances. For the enstrophy, tube-like structures at an intermediate scale are primarily surrounded by sheets of smaller scales of the enstrophy and structures of dissipation at the same and smaller scales. A secondary contribution results from tubes of enstrophy at smaller scales appearing at farther distances. Different configurations of composite structures are presented.

Type
Papers
Information
Journal of Fluid Mechanics , Volume 620 , 10 February 2009 , pp. 121 - 166
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ashurst, W. T., Kerstein, A. R., Kerr, R. M. & Gibson, C. H. 1987 Alignment of vorticity and scalar gradient with strain rate in simulated Navier-Stokes turbulence. Phys. Fluids 30, 2343–2353.CrossRefGoogle Scholar
Batchelor, G. K. & Townsend, A. A. 1949 The nature of turbulent motion at large wavenumbers. Proc. R. Soc. Lond. A 199, 238–255.Google Scholar
Bermejo-Moreno, I. & Pullin, D. I. 2008 On the non-local geometry of turbulence. J. Fluid Mech. 603, 101–135.CrossRefGoogle Scholar
Bradshaw, P. & Koh, Y. M. 1981 A note on Poisson's equation for pressure in a turbulent flow. Phys. Fluids 24, 777.CrossRefGoogle Scholar
Brasseur, J. G. & Wang, Q. 1992 Structural evolution of intermittency and anisotropy at different scales analyzed using three-dimensional wavelet transforms. Phys. Fluids A 4, 2538–2554.CrossRefGoogle Scholar
Candès, E., Demanet, L., Donoho, D. & Ying, L. 2005 Fast discrete curvelet transforms. Multiscale Model Simul. 5, 861–899.CrossRefGoogle Scholar
Chen, S., Sreenivasan, K. R. & Nelkin, M. 1997 Inertial range scalings of dissipation and enstrophy in isotropic turbulence. Phys. Rev. Lett. 79, 1253–1256.CrossRefGoogle Scholar
Goto, Susumu 2008 A physical mechanism of the energy cascade in homogeneous isotropic turbulence. J. Fluid Mech. 605, 355–266.CrossRefGoogle Scholar
Hamlington, P. E., Schumacher, J. & Dahm, W. J. A. 2008 Local and nonlocal strain rate fields and vorticity alignment in turbulent flows. Phys. Rev. E 77, 026303.CrossRefGoogle ScholarPubMed
He, G., Chen, S., Kraichan, R. H., Zhang, R. & Zhou, Y. 1998 Statistics of dissipation and enstrophy induced by localized vortices. Phys. Rev. Lett. 81, 4639.CrossRefGoogle Scholar
Horiuti, K. 2001 A classification method for vortex sheet and tube structures in turbulent flows. Phys. Fluids A 13 (12), 3756–3774.CrossRefGoogle Scholar
Horiuti, K. & Fujisawa, T. 2008 The multi-mode stretched spiral vortex in homogeneous isotropic turbulence. J. Fluid Mech. 595, 341–366.CrossRefGoogle Scholar
Horiuti, K. & Takagi, Y. 2005 Identification method for vortex sheet structures in turbulent flows. Phys. Fluids 17 (12), 121703.CrossRefGoogle Scholar
Hunt, J. C. R., Wray, A. A. & Moin, P. 1988 Eddies, stream, and convergence zones in turbulent flows. Tech. Rep. Center for Turbulence Research Report CTR-S88.Google Scholar
Ishihara, T., Kaneda, Y., Yokokawa, M., Itakura, K. & Uno, A. 2003 Spectra of energy dissipation, enstrophy and pressure by high-resolution direct numerical simulations of turbulence in a periodic box. J. Phys. Soc. Japan 72, 983–986.CrossRefGoogle Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.Google Scholar
Jiménez, J. 1992 Kinematic alignment effects in turbulent flows. Phys. Fluids A 4, 652–654.CrossRefGoogle Scholar
Jiménez, J., Wray, A. W., Saffman, P. G. & Rogallo, R. S. 1993 The structure of intense vorticity in isotropic turbulence. J. Fluid Mech. 255, 65–90.CrossRefGoogle Scholar
Kennedy, D. A. & Corrsin, S. 1961 Spectral flatness factor and intermittency in turbulence and in non-linear noise. J. Fluid Mech. 10, 366–370.CrossRefGoogle Scholar
Kerr, R. M. 1985 Higher-order derivative correlations and the alignment of small-scale structures in isotropic numerical turbulence. J. Fluid Mech. 153, 31–58.CrossRefGoogle Scholar
Koenderink, J. J. & van Doorn, A. J. 1992 Surface shape and curvature scales. Image Vision Comput. 10 (8), 557–565.CrossRefGoogle Scholar
Kolmogorov, A. N. 1941 a Dissipation of energy in a locally isotropic turbulence. Dokl. Nauk. SSSR. 32, 16–18.Google Scholar
Kolmogorov, A. N. 1941 b The local structure of turbulence in incompressible viscous fluids at very large Reynolds numbers. Dokl. Nauk. SSSR. 30, 301–305.Google Scholar
Kolmogorov, A. N. 1962 A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds numbers. J. Fluid Mech. 13, 82–85.CrossRefGoogle Scholar
Kraichnan, R. H. 1974 On Kolmogorov's inertial-range theories. J. Fluid Mech. 62, 305–330.CrossRefGoogle Scholar
Landau, L. D. & Lifshitz, E. M. 1959 Fluid Mechanics. Pergamon.Google Scholar
Lundgren, T. S. 1982 Strained spiral vortex model for turbulent fine structure. Phys. Fluids 25, 2193–2203.CrossRefGoogle Scholar
Meneveau, C. 1991 Analysis of turbulence in the orthonormal wavelet representation. J. Fluid Mech. 232, 469–520.CrossRefGoogle Scholar
Misra, A. & Pullin, D. I. 1997 A vortex-based subgrid stress model for large-eddy simulations. Phys. Fluids 9, 2443–2454.CrossRefGoogle Scholar
Moisy, F. & Jiménez, J. 2004 Geometry and clustering of intense structures in isotropic turbulence. J. Fluid Mech. 513, 111–133.Google Scholar
Nomura, K. K. & Post, G. K. 1998 The structure and dynamics of vorticity and rate of strain in incompressible homogeneous turbulence. J. Fluid Mech. 377, 65–97.CrossRefGoogle Scholar
Okamoto, N., Yoshimatsu, K., Shneider, K., Farge, M. & Kaneda, Y. 2007 Coherent vortices in high resolution direct numerical simulation of homogeneous isotropic turbulence: A wavelet viewpoint. Phys. Fluids 19, 115109.CrossRefGoogle Scholar
Onsager, L. 1945 The distribution of energy in turbulence. Phys. Rev. 68, 286.Google Scholar
Pullin, D. I. & Saffman, P. G. 1997 Vortex dynamics in turbulence. Annu. Rev. Fluid Mech. 30, 31–51.CrossRefGoogle Scholar
Richardson, L. F. 1922 Weather Prediction by Numerical Process. Cambridge University Press.Google Scholar
Richardson, L. F. 1926 Atmospheric diffusion shown on a distance-neighbor graph. Proc. R. Soc. Lond. Ser. A 110, 709–737.Google Scholar
Ruetsch, G. R. & Maxey, M. R. 1992 The evolution of small-scale structures in isotropic homogeneous turbulence. Phys. Fluids A 4 (12), 2747–2760.CrossRefGoogle Scholar
Schumacher, J., Sreenivasan, K. R. & Yeung, P. K. 2005 Very fine structures in scalar mixing. J. Fluid Mech. 531, 113–122.CrossRefGoogle Scholar
Siggia, E. D. 1981 Numerical study of small-scale intermittency in three-dimensional turbulence. J. Fluid Mech. 107, 375–406.CrossRefGoogle Scholar
Sreenivasan, K. R. 2004 Possible effects of small-scale intermittency in turbulent reacting flows. Flow, Turbul. Combus. 72, 115–131.CrossRefGoogle Scholar
Sreenivasan, K. R. & Meneveau, C. 1988 Singularities of the the equations of fluid motion. Phys. Rev. A 38, 6287–6295.CrossRefGoogle ScholarPubMed
Tanaka, M. & Kida, S. 1993 Characterization of vortex tubes and sheets. Phys. Fluids A 5, 2079–2082.CrossRefGoogle Scholar
Tao, B., Katz, J. & Meneveau, C. 2000 Geometry and scale relationships in high Reynolds number turbulence determined from three-dimensional holographic velocimetry. Phys. Fluids 12, 941–944.CrossRefGoogle Scholar
Tsinober, A., Kit, E. & Dracos, T. 1992 Experimental investigation of the field of velocity-gradients in turbulent flows. J. Fluid Mech. 242, 169–192.CrossRefGoogle Scholar
Vincent, A. & Meneguzzi, M. 1994 The dynamics of vorticity tubes in homogeneous turbulence. J. Fluid Mech. 258, 245–254.CrossRefGoogle Scholar
Wang, L. & Peters, N. 2006 The length-scale distribution function of the distance between extremal points in passive scalar turbulence. J. Fluid. Mech. 554, 457–475.CrossRefGoogle Scholar
Wu, J-Z., Zhou, Y. & Fan, M. 1999 A note on kinetic energy, dissipation and enstrophy. Phys. Fluids 11, 503–505.Google Scholar
Zeff, B. W., Lanterman, D. D., McAllister, R., Roy, R., Kostelich, E. J. & Lathrop, D. P. 2003 Measuring intense rotation and dissipation in turbulent flows. Nature 421, 146–149.CrossRefGoogle ScholarPubMed