Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Sugie, Jitsuro
and
Endo, Ayano
2009.
Attractivity for two-dimensional linear systems whose anti-diagonal coefficients are periodic.
Proceedings of the American Mathematical Society,
Vol. 137,
Issue. 12,
p.
4117.
Sugie, Jitsuro
Hata, Saori
and
Onitsuka, Masakazu
2010.
Global attractivity for half-linear differential systems with periodic coefficients.
Journal of Mathematical Analysis and Applications,
Vol. 371,
Issue. 1,
p.
95.
Sugie, Jitsuro
and
Onitsuka, Masakazu
2010.
Integral conditions on the uniform asymptotic stability for two-dimensional linear systems with time-varying coefficients.
Proceedings of the American Mathematical Society,
Vol. 138,
Issue. 7,
p.
2493.
Saito, Yasuhisa
Sugie, Jitsuro
and
Lee, Yong-Hoon
2011.
Global asymptotic stability for predator–prey models with environmental time-variations.
Applied Mathematics Letters,
Vol. 24,
Issue. 12,
p.
1973.
Sugie, Jitsuro
2011.
Global asymptotic stability for damped half-linear oscillators.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 74,
Issue. 18,
p.
7151.
Sugie, Jitsuro
2011.
Three-dimensional time-varying nonlinear systems containing a Hamilton system.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 74,
Issue. 6,
p.
2296.
Hata, S.
and
Sugie, J.
2013.
A necessary and sufficient condition for the global asymptotic stability of damped half-linear oscillators.
Acta Mathematica Hungarica,
Vol. 138,
Issue. 1-2,
p.
156.
Sugie, Jitsuro
2013.
Smith-type criterion for the asymptotic stability of a pendulum with time-dependent damping.
Proceedings of the American Mathematical Society,
Vol. 141,
Issue. 7,
p.
2419.
Sugie, Jitsuro
and
Onitsuka, Masakazu
2014.
Growth conditions for uniform asymptotic stability of damped oscillators.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 98,
Issue. ,
p.
83.
Sugie, Jitsuro
and
Kira, Kazuya
2015.
Uniform global asymptotic stability for oscillators with superlinear damping.
Journal of Mathematical Analysis and Applications,
Vol. 425,
Issue. 2,
p.
827.
Zheng, Wei
and
Sugie, Jitsuro
2016.
Parameter diagram for global asymptotic stability of damped half-linear oscillators.
Monatshefte für Mathematik,
Vol. 179,
Issue. 1,
p.
149.
Ishihara, Kazuki
and
Sugie, Jitsuro
2017.
Uniform asymptotic stability of time-varying damped harmonic oscillators.
Proceedings of the American Mathematical Society, Series B,
Vol. 4,
Issue. 4,
p.
31.
Sugie, Jitsuro
and
Ishihara, Kazuki
2019.
Sufficient conditions for convergence of solutions of damped elliptic equations.
Monatshefte für Mathematik,
Vol. 189,
Issue. 3,
p.
441.
Şahan, Gökhan
2023.
Exponential stability and boundedness of nonlinear perturbed systems by unbounded perturbation terms.
Journal of the Franklin Institute,
Vol. 360,
Issue. 13,
p.
10275.
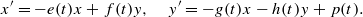 The primary goal is to establish conditions on time-varying coefficients e(t), f(t), g(t) and h(t) and a forcing term p(t) for all solutions to converge to the origin (0,0) as
The primary goal is to establish conditions on time-varying coefficients e(t), f(t), g(t) and h(t) and a forcing term p(t) for all solutions to converge to the origin (0,0) as 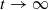 . Here, the zero solution of the corresponding homogeneous linear system is assumed to be neither uniformly stable nor uniformly attractive. Sufficient conditions are given for asymptotic stability of the zero solution of the nonlinear perturbed system
. Here, the zero solution of the corresponding homogeneous linear system is assumed to be neither uniformly stable nor uniformly attractive. Sufficient conditions are given for asymptotic stability of the zero solution of the nonlinear perturbed system 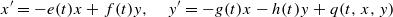 under the assumption that q(t,0,0)=0.
under the assumption that q(t,0,0)=0.



