Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Dekking, Michel
2009.
Fractal Geometry and Stochastics IV.
Vol. 61,
Issue. ,
p.
269.
Feng, De-Jun
and
Wang, Yang
2009.
On the structures of generating iterated function systems of Cantor sets.
Advances in Mathematics,
Vol. 222,
Issue. 6,
p.
1964.
Oberlin, Daniel M.
2010.
Lower Bounds for Dimensions of Sums of Sets.
Journal of Geometric Analysis,
Vol. 20,
Issue. 2,
p.
422.
Lima, Yuri
and
Moreira, Carlos Gustavo
2011.
Yet another proof of Marstrand’s theorem.
Bulletin of the Brazilian Mathematical Society, New Series,
Vol. 42,
Issue. 2,
p.
331.
Nazarov, Fedor
Peres, Yuval
and
Shmerkin, Pablo
2012.
Convolutions of cantor measures without resonance.
Israel Journal of Mathematics,
Vol. 187,
Issue. 1,
p.
93.
Yao, Yuanyuan
and
Li, Wenxia
2012.
Self-similar structure on intersection of Cartesian product of Cantor triadic sets with their translations.
Monatshefte für Mathematik,
Vol. 166,
Issue. 3-4,
p.
591.
Hochman, Michael
and
Shmerkin, Pablo
2012.
Local entropy averages and projections of fractal measures.
Annals of Mathematics,
Vol. 175,
Issue. 3,
p.
1001.
Marchetti, Domingos H. U.
and
Wreszinski, Walter F.
2012.
Anderson-like Transition for a Class of Random Sparse Models in d≥2 Dimensions.
Journal of Statistical Physics,
Vol. 146,
Issue. 5,
p.
885.
Shmerkin, Pablo
2014.
On the Exceptional Set for Absolute Continuity of Bernoulli Convolutions.
Geometric and Functional Analysis,
Vol. 24,
Issue. 3,
p.
946.
Mattila, Pertti
2014.
Geometry and Analysis of Fractals.
Vol. 88,
Issue. ,
p.
283.
RAMS, MICHAŁ
and
SIMON, KÁROLY
2015.
Projections of fractal percolations.
Ergodic Theory and Dynamical Systems,
Vol. 35,
Issue. 2,
p.
530.
Falconer, Kenneth
Fraser, Jonathan
and
Jin, Xiong
2015.
Fractal Geometry and Stochastics V.
Vol. 70,
Issue. ,
p.
3.
Ferguson, Andrew
Fraser, Jonathan M.
and
Sahlsten, Tuomas
2015.
Scaling scenery of (×m,×n) invariant measures.
Advances in Mathematics,
Vol. 268,
Issue. ,
p.
564.
Yao, Yuanyuan
2015.
Generating iterated function systems of some planar self-similar sets.
Journal of Mathematical Analysis and Applications,
Vol. 421,
Issue. 1,
p.
938.
Damanik, David
Gorodetski, Anton
and
Solomyak, Boris
2015.
Absolutely continuous convolutions of singular measures and an application to the square Fibonacci Hamiltonian.
Duke Mathematical Journal,
Vol. 164,
Issue. 8,
Hochman, Michael
and
Shmerkin, Pablo
2015.
Equidistribution from fractal measures.
Inventiones mathematicae,
Vol. 202,
Issue. 1,
p.
427.
Falconer, Kenneth
and
Jin, Xiong
2015.
Dimension Conservation for Self-Similar Sets and Fractal Percolation.
International Mathematics Research Notices,
Vol. 2015,
Issue. 24,
p.
13260.
Hochman, Michael
2015.
Lectures on dynamics, fractal geometry, and metric number theory.
Journal of Modern Dynamics,
Vol. 8,
Issue. 3/4,
p.
437.
Orponen, Tuomas
2015.
On the packing dimension and category of exceptional sets of orthogonal projections.
Annali di Matematica Pura ed Applicata (1923 -),
Vol. 194,
Issue. 3,
p.
843.
Shmerkin, Pablo
2015.
Fractal Geometry and Stochastics V.
Vol. 70,
Issue. ,
p.
53.
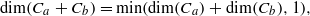 where dim is Hausdorff dimension. More generally, given two self-similar sets K,K′ in ℝ and a scaling parameter s>0, if the dimension of the arithmetic sum K+sK′ is strictly smaller than dim (K)+dim (K′)≤1 (‘geometric resonance’), then there exists r<1 such that all contraction ratios of the similitudes defining K and K′ are powers of r (‘algebraic resonance’). Our method also yields a new result on the projections of planar self-similar sets generated by an iterated function system that includes a scaled irrational rotation.
where dim is Hausdorff dimension. More generally, given two self-similar sets K,K′ in ℝ and a scaling parameter s>0, if the dimension of the arithmetic sum K+sK′ is strictly smaller than dim (K)+dim (K′)≤1 (‘geometric resonance’), then there exists r<1 such that all contraction ratios of the similitudes defining K and K′ are powers of r (‘algebraic resonance’). Our method also yields a new result on the projections of planar self-similar sets generated by an iterated function system that includes a scaled irrational rotation.



