Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Trif, Tiberiu
2000.
Meyer-König and Zeller operators based on the \(q\)-integers.
Journal of Numerical Analysis and Approximation Theory,
Vol. 29,
Issue. 2,
p.
221.
Oruç, Halil
and
Tuncer, Necibe
2002.
On the Convergence and Iterates of q-Bernstein Polynomials.
Journal of Approximation Theory,
Vol. 117,
Issue. 2,
p.
301.
Il'inskii, Alexander
and
Ostrovska, Sofiya
2002.
Convergence of Generalized Bernstein Polynomials.
Journal of Approximation Theory,
Vol. 116,
Issue. 1,
p.
100.
Kryakin, Yuri
and
Trebels, Walter
2002.
q-Moduli of Continuity in Hp(D), p>0, and an Inequality of Hardy and Littlewood.
Journal of Approximation Theory,
Vol. 115,
Issue. 2,
p.
238.
Oruç, Halil
and
Phillips, George M.
2003.
q-Bernstein polynomials and Bézier curves.
Journal of Computational and Applied Mathematics,
Vol. 151,
Issue. 1,
p.
1.
Ostrovska, Sofiya
2003.
q-Bernstein polynomials and their iterates.
Journal of Approximation Theory,
Vol. 123,
Issue. 2,
p.
232.
Oruç, Halil
and
Akmaz, Hakan K.
2004.
Symmetric functions and the Vandermonde matrix.
Journal of Computational and Applied Mathematics,
Vol. 172,
Issue. 1,
p.
49.
Heping, Wang
2005.
Korovkin-type theorem and application.
Journal of Approximation Theory,
Vol. 132,
Issue. 2,
p.
258.
Sablonnière, Paul
2005.
Trends and Applications in Constructive Approximation.
p.
229.
Doğru, Ogün
and
Gupta, Vijay
2006.
Korovkin-type approximation properties of bivariate q-Meyer-König and Zeller operators.
Calcolo,
Vol. 43,
Issue. 1,
p.
51.
Dişibüyük, Çetin
and
Oruç, Halil
2007.
A generalization of rational Bernstein–Bézier curves.
BIT Numerical Mathematics,
Vol. 47,
Issue. 2,
p.
313.
Aral, Ali
and
Doğru, Ogün
2007.
Bleimann, Butzer, and Hahn Operators Based on the -Integers.
Journal of Inequalities and Applications,
Vol. 2007,
Issue. 1,
p.
079410.
Xiang, Xueyan
He, Qian
and
Yang, Wenshan
2007.
Convergence rate for iterates of q-Bernstein polynomials.
Analysis in Theory and Applications,
Vol. 23,
Issue. 3,
p.
243.
Ostrovska, Sofiya
2007.
The approximation of logarithmic function by q-Bernstein polynomials in the case q > 1.
Numerical Algorithms,
Vol. 44,
Issue. 1,
p.
69.
Dişibüyük, Çetin
and
Oruç, Halil
2008.
Tensor product q-Bernstein polynomials.
BIT Numerical Mathematics,
Vol. 48,
Issue. 4,
p.
689.
Zhu, Laiyi
and
Lin, Qiu
2009.
Saturation theorems for generalized Bernstein polynomials.
Analysis in Theory and Applications,
Vol. 25,
Issue. 3,
p.
242.
Nowak, Grzegorz
2009.
Approximation properties for generalized q-Bernstein polynomials.
Journal of Mathematical Analysis and Applications,
Vol. 350,
Issue. 1,
p.
50.
Yousefi, S.A.
2009.
Finding a control parameter in a one-dimensional parabolic inverse problem by using the Bernstein Galerkin method.
Inverse Problems in Science and Engineering,
Vol. 17,
Issue. 6,
p.
821.
Simsek, Yilmaz
and
Acikgoz, Mehmet
2010.
A New Generating Function of (q-) Bernstein-Type Polynomials and Their Interpolation Function.
Abstract and Applied Analysis,
Vol. 2010,
Issue. ,
p.
1.
Charalambides, Charalambos A.
2010.
The q-Bernstein basis as a q-binomial distribution.
Journal of Statistical Planning and Inference,
Vol. 140,
Issue. 8,
p.
2184.
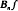 , where 0 < q ≤ 1. This paper summarizes briefly the previously known results concerning these generalized Bernstein polynomials and gives new results concerning
, where 0 < q ≤ 1. This paper summarizes briefly the previously known results concerning these generalized Bernstein polynomials and gives new results concerning 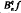 when f is a monomial. The main results of the paper are obtained by using the concept of total positivity. It is shown that if f is increasing then
when f is a monomial. The main results of the paper are obtained by using the concept of total positivity. It is shown that if f is increasing then 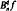 is increasing, and if f is convex then
is increasing, and if f is convex then 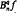 is convex, generalizing well known results when q = 1. It is also shown that if f is convex then, for any positive integer n
is convex, generalizing well known results when q = 1. It is also shown that if f is convex then, for any positive integer n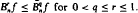 This supplements the well known classical result that
This supplements the well known classical result that 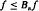 when f is convex.
when f is convex.



