Article contents
Lacunary Müntz systems
Published online by Cambridge University Press: 20 January 2009
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
The classical theorem of Müntz and Szász says that the span of
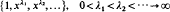
is dense in C[0,1] in the uniform norm if and only if 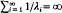 . We prove that, if {λi} is lacunary, we can replace the underlying interval [0,1] by any set of positive measure. The key to the proof is the establishment of a bounded Remez-type inequality for lacunary Müntz systems. Namely if A ⊆ [0,1] and its Lebesgue measure µ(A) is at least ε > 0 then
. We prove that, if {λi} is lacunary, we can replace the underlying interval [0,1] by any set of positive measure. The key to the proof is the establishment of a bounded Remez-type inequality for lacunary Müntz systems. Namely if A ⊆ [0,1] and its Lebesgue measure µ(A) is at least ε > 0 then
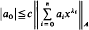
where c depends only on ε and Λ (not on n and A) and where Λ:=infiλi+1/λi>1.
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 36 , Issue 3 , October 1993 , pp. 361 - 374
- Copyright
- Copyright © Edinburgh Mathematical Society 1993
References
REFERENCES
1.Borwein, P. B., Zeros of Chebyshev polynomials in Markov systems, J. Approx. Theory 63 (1990), 56–64.CrossRefGoogle Scholar
2.Borwein, P. B. and Saff, E., On the denseness of weighted incomplete approximations, in Gonchar, A. A. and Saff, E. B. (Eds.), Progress in Approximation Theory (Springer-Verlag, 1992), 419–429.CrossRefGoogle Scholar
3.Borwein, P. B., Variations on Müntz's theme, Canad. Math. Bull. 34 (1991), 305–310.CrossRefGoogle Scholar
5.Clarkson, J. A. and Erdös, P., Approximation by polynomials, Duke Math J. 10 (1943), 5–11.CrossRefGoogle Scholar
6.Erdélyi, T., Remez-type inequalities on the size of generalized polynomials, J. London Math. Soc. 45 (1992), 255–264.CrossRefGoogle Scholar
7.Feinerman, R. P. and Newman, D. J., Polynomial Approximation (Williams and Wilkins, Baltimore, MD, 1976).Google Scholar
8.Von Golitschek, M., A short proof of Müntz's theorem, J. Approx. Theory 39 (1983), 394–395.CrossRefGoogle Scholar
9.Hirschman, I. I. Jr., Approximation by non-dense sets of functions, Ann. of Math. 50 (1949), 666–675.CrossRefGoogle Scholar
11.McCarthy, P. C., Sayre, J. E. and Shawyer, B. L. R., Generalized Legendre polynomials, manuscript.Google Scholar
12.Newman, D. J., Derivative bounds for Müntz polynomials, J. Approx. Theory 18 (1976), 360–362.CrossRefGoogle Scholar
13.Newman, D. J., Approximation with rational functions, Regional Conference Series in Mathematics 41 (1978).Google Scholar
15.Smith, P. W., An improvement theorem for Descartes systems, Proc. Amer. Math. Soc. 70 (1978), 26–30.CrossRefGoogle Scholar
16.Trent, T. T., A Müntz-Szász theorem for C(D), Proc. Amer. Math. Soc. 83 (1981), 296–298.Google Scholar
- 3
- Cited by




