Article contents
Explicit evaluation of Euler sums
Published online by Cambridge University Press: 20 January 2009
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
In response to a letter from Goldbach, Euler considered sums of the form
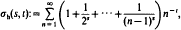
where s and t are positive integers.
As Euler discovered by a process of extrapolation (from s + t ≦ 13), σh(s, t) can be evaluated in terms of Riemann ζ-functions when s + t is odd. We provide a rigorous proof of Euler's discovery and then give analogous evaluations with proofs for corresponding alternating sums. Relatedly we give a formula for the series
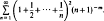
This evaluation involves ζ-functions and σh(2, m).
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1995
References
REFERENCES
1.Bailey, D. H., Borwein, J. and Girgensohn, R., Experimental evaluation of Euler sums, Experiment. Math. 3 (1994), 17–30.CrossRefGoogle Scholar
2.Berndt, B. C., Ramanujan's Notebooks, Part I(Springer-Verlag, New York, 1985).CrossRefGoogle Scholar
3.Borwein, D., Borwein, J. M., On an intriguing integral and some series related to ζ(4), Proc. Amer. Math. Soc., to appear.Google Scholar
4.De Doelder, P. J., On some series containing Ψ(x) — Ψ(y) and (Ψ(x)—Ψ(y))2 for certain values of x and y, J. Comput. Appl. Math. 37 (1991), 125–141.CrossRefGoogle Scholar
6.Hoffman, M., Multiple harmonic series, Pacific J. Math. 152 (1992), 275–290.CrossRefGoogle Scholar
9.Rao, R. Sitaramachandra, Subbarao, M. V., Transformation formulae for multiple series, Pacific J. Math. 113 (1984), 471–479.Google Scholar
10.Rao, R. Sitaramachandra, A formula of S. Ramanujan, J. Number Theory 25 (1987), 1–19.Google Scholar
- 122
- Cited by




