Article contents
Topology and growth of a special class of holomorphic self-maps of ℂ*
Published online by Cambridge University Press: 19 September 2008
Abstract
It is a general problem to find appropriate sets of moduli for families of functions that generate dynamical systems. In this paper we solve this problem for a specific family of holomorphic self-maps of ℂ* defined by
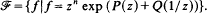
The main theorem states that any function topologically conjugate to a member of ℱ is holomorphically conjugate to some member of the family. It follows that the coefficients of the polynomials P(z) and Q(z) are a suitable set of moduli for the families of dynamical systems generated by these functions.
The moduli spaces of functions in ℱ are easy to study computationally and have been studied by many authors. (See references in the text.)
- Type
- Research Article
- Information
- Copyright
- Copyright © Cambridge University Press 1989
References
REFERENCES
- 3
- Cited by




