Ergodic Theory and Dynamical Systems

Table of Contents - 01 June 1984 - Volume 4, Issue 02  

Research Article

The entropies of topological Markov shifts and a related class of algebraic integers

D. A. Linda1

a1 Department of Mathematics, University of Washington, Seattle, Washington 98195, USA

Abstract

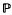We give an algebraic characterization of the class S0143385700002443_xs02119 of spectral radii of aperiodic non-negative integral matrices, and describe a method of constructing all such matrices with given spectral radius. The logarithms of the numbers in 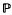S0143385700002443_xs02119 are the entropies of mixing topological Markov shifts. There is an arithmetic structure to 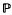S0143385700002443_xs02119, including factorization into irreducibles in only finitely many ways. This arithmetic structure has dynamical consequences, such as the impossibility of factoring the p-shift into a direct product of nontrivial homeomorphisms for prime p.

(Received October 06 1983)