On braid monodromies of non-simple braided surfaces
Published online by Cambridge University Press: 24 October 2008
Extract
A braided surface of degree m is a compact oriented surface S embedded in a bidisk 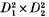 such that
such that 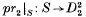 is a branched covering map of degree m and
is a branched covering map of degree m and 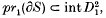 , where
, where 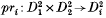 is the projection. It was defined L. Rudolph [14, 16] with some applications to knot theory, cf. [13, 14, 15, 16, 17, 18]. A similar notion was defined O. Ya. Viro: A (closed) 2-dimensional braid in R4 is a closed oriented surface F embedded in R4 such that
is the projection. It was defined L. Rudolph [14, 16] with some applications to knot theory, cf. [13, 14, 15, 16, 17, 18]. A similar notion was defined O. Ya. Viro: A (closed) 2-dimensional braid in R4 is a closed oriented surface F embedded in R4 such that 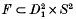 and pr2 │F: F → S2 is a branched covering map, where
and pr2 │F: F → S2 is a branched covering map, where 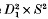 is the tubular neighbourhood of a standard 2-sphere in R4. It is related to 2-knot theory, cf. [8, 9, 10]. Braided surfaces and 2-dimensional braids are called simple if their associated branched covering maps are simple. Simple braided surfaces and simple 2-dimensional braids are investigated in some articles, [5, 8, 9, 14, 16], etc. This paper treats of non-simple braided surfaces in the piecewise linear category. For braided surfaces a natural weak equivalence relation, called braid ambient isotopy, appears essentially although it is not important for classical dimensionai braids Artin's argument [1].
is the tubular neighbourhood of a standard 2-sphere in R4. It is related to 2-knot theory, cf. [8, 9, 10]. Braided surfaces and 2-dimensional braids are called simple if their associated branched covering maps are simple. Simple braided surfaces and simple 2-dimensional braids are investigated in some articles, [5, 8, 9, 14, 16], etc. This paper treats of non-simple braided surfaces in the piecewise linear category. For braided surfaces a natural weak equivalence relation, called braid ambient isotopy, appears essentially although it is not important for classical dimensionai braids Artin's argument [1].
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 120 , Issue 2 , August 1996 , pp. 237 - 245
- Copyright
- Copyright © Cambridge Philosophical Society 1996
References
REFERENCES
- 6
- Cited by




