On epimorphisms of non-commutative rings
Published online by Cambridge University Press: 24 October 2008
Extract
From a commutative ring A, Lazard(8) has made a flat injective epimorphism: A → B of commutative rings, such that if A → C is another flat injective epimorphism of commutative rings, then there is one and only one ring morphism: B → C such that the diagram
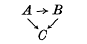
commutes; and he shows too that B → C is a flat injective epimorphism. The main aim of the present paper is to make a similar object for not necessarily commutative rings: this is achieved thanks to the notion of an A-prering, intermediate between that of an A-bimodule and that of an A-ring. In passing, prerings are also used to construct a kind of non-commutative ring of fractions.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 68 , Issue 3 , November 1970 , pp. 589 - 600
- Copyright
- Copyright © Cambridge Philosophical Society 1970
References
REFERENCES
- 8
- Cited by




