Hostname: page-component-8448b6f56d-tj2md Total loading time: 0 Render date: 2024-04-18T04:30:17.867Z Has data issue: false hasContentIssue false
  • English
  • Français

Superoptimal approximation by meromorphic functions

Published online by Cambridge University Press:  24 October 2008

V. V. Peller  and
N. J. Young
V. V. Peller
Affiliation:
Department of Mathematics, Kansas State University, Manhattan, Kansas 66502, U.S.A.
N. J. Young
Affiliation:
Department of Mathematics and Statistics, Lancaster University, Lancaster, LA1 4YF
Get access Rights & Permissions [Opens in a new window]

Abstract

Let G be a matrix function of type m × n and suppose that G is expressible as the sum of an H∞ function and a continuous function on the unit circle. Suppose also that the (k – 1)th singular value of the Hankel operator with symbol G is greater than the kth singular value. Then there is a unique superoptimal approximant to G in 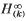: that is, there is a unique matrix function Q having at most k poles in the open unit disc which minimizes s∞(G – Q) or, in other words, which minimizes the sequence

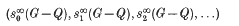
with respect to the lexicographic ordering, where

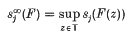
and Sj(·) denotes the jth singular value of a matrix. This result is due to the present authors [PY1] in the case k = 0 (when the hypothesis on the Hankel singular values is vacuous) and to S. Treil[T2] in general. In this paper we give a proof of uniqueness by a diagonalization argument, a high level algorithm for the computation of the superoptimal approximant and a recursive parametrization of the set of all optimal solutions of a matrix Nehari—Takagi problem.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 119 , Issue 3 , April 1996 , pp. 497 - 511
Copyright
Copyright © Cambridge Philosophical Society 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[AAK]Adamyan, V. M., Arov, D. Z. and Kreim, M. G.. Infinite Hankel block matrices and some related continuation problems, Izv. Akad. Nauk Armyan. SSR Ser.Mat 6 (1971), 87–112.Google Scholar
[BGR]Ball, J. A., Gohberg, I. and Rodman, L.. Interpolation of rational matrix functions (Birkhäuser Verlag, 1990).CrossRefGoogle Scholar
[BH1]Ball, J. A. and Helton, J. W.. A Beurling-Lax theorem for the Lie group U(m, n) which contains most classical interpolation theory. J. Operator Theory 9 (1983), 107–142.Google Scholar
[BH2]Ball, J. A. and Helton, J. W.. Interpolation problems of Pick-Nevanlinna and Loewner types for meromorphic matrix functions: parametrisation of the set of all solutions. Integral Equations and Operator Theory 9 (1986), 155–203.CrossRefGoogle Scholar
[G1]Glover, K.. All optimal Hankel-norm approximations of linear multivariable systems and their L ∞ error bounds. Int. J. Control 39 (1984), 1115–1193.CrossRefGoogle Scholar
[G2]Glover, K.. A tutorial on Hankel-norm approximation; in: From data to model, ed. Willems, J. C. (Springer-Verlag, 1989).Google Scholar
[He]Helson, H.. Lectures on invariant subspaces (Academic Press, 1964).Google Scholar
[Ho]Hoffman, K.. Banach spaces of analytic functions (Prentice Hall, 1962).Google Scholar
[KL]Kung, S. Y. and Lin, D. W.. Optimal Hankel-norm model reduction: multivariable systems. IEEE Trans. Automatic Control 26 (1981), 832–852.CrossRefGoogle Scholar
[P]Partington, J. R.. An introduction to Hankel operators (Cambridge University Press, 1988).Google Scholar
[PK]Peller, V. V. and Khruschev, S. V.. Hankel operators, best approximation and stationary Gaussian processes. Russian Math. Surveys 37 (1982), 53–124.CrossRefGoogle Scholar
[PY1]Peller, V. V. and Young, N. J.. Superoptimal analytic approximations of matrix functions. J. Functional Analysis 120 (1994), 300–343.CrossRefGoogle Scholar
[PY2]Peller, V. V. and Young, N. J.. Superoptimal model reduction for continuous time systems. Technical Report 94/94, Lancaster University Mathematics and Statistics Department.Google Scholar
[PY3]Peller, V. V. and Young, N. J.. Construction of superoptimal approximants (to be published in Mathematics of Communications, Systems and Control).Google Scholar
[T1]Treil, S. R.. The Adamyan-Arov-Krein theorem: a vector version. Zap. Nauchn. Semin. LOMI 141 (1985), 56–71 (Russian).Google Scholar
[T2]Treil, S. R.. On superoptimal approximation by analytic and meromorphic matrix-valued functions. J. Functional Analysis(to appear).Google Scholar
[Yl]Young, N. J.. The Nevanlinna-Pick problem for matrix-valued functions. J. Operator Theory 15 (1986), 239–265.Google Scholar
[Y2]Young, N. J.. Superoptimal Hankel norm approximations; in: Modelling, robustness and sensitivity reduction in control systems, ed. Curtain, R. F. (Springer-Verlag, 1987).Google Scholar
[Y3]Young, N. J.. The Nehari problem and optimal Hankel norm approximation; in: Analysis and optimization of systems: state and frequency domain approaches for infinite-dimensional systems, edited by Curtain, R. F. et al. Springer Lecture Notes in Control and Information Sciences No. 185 (1993), 199–221.Google Scholar