Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Lawrence, R. J.
1995.
Asymptotic expansions of Witten–Reshetikhin–Turaev invariants for some simple 3-manifolds.
Journal of Mathematical Physics,
Vol. 36,
Issue. 11,
p.
6106.
Le, Thang Q. T.
Murakami, Hitoshi
Murakami, Jun
and
Ohtsuki, Tomotada
1995.
A three-manifold invariant derived from the universal Vassiliev-Kontsevich invariant.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 71,
Issue. 6,
Ohtsuki, Tomotada
1996.
A polynomial invariant of rational homology 3-spheres.
Inventiones Mathematicae,
Vol. 123,
Issue. 1,
p.
241.
Karowski, Michael
Schrader, Robert
and
Vogt, Elmar
1997.
Invariants of Three-Manifolds, Unitary Representations of the Mapping Class Group, and Numerical Calculations.
Experimental Mathematics,
Vol. 6,
Issue. 4,
p.
317.
Boden, Hans U.
and
Herald, Christopher M.
1998.
The $\rm{SU}(3)$ Casson invariant for integral homology 3-spheres.
Journal of Differential Geometry,
Vol. 50,
Issue. 1,
Rozansky, L.
1998.
On p-adic convergence of perturbative
invariants of some rational homology spheres.
Duke Mathematical Journal,
Vol. 91,
Issue. 2,
Lescop, Christine
1998.
European Congress of Mathematics.
Vol. 168,
Issue. ,
p.
296.
Lin, Xiaosong
and
Wang, Zhenghan
1999.
On ohtsuki’s invariants of integral homology 3-spheres.
Acta Mathematica Sinica,
Vol. 15,
Issue. 3,
p.
293.
Le, Thang T. Q.
2000.
Integrality and symmetry of quantum link invariants.
Duke Mathematical Journal,
Vol. 102,
Issue. 2,
Sato, Chifumi
2001.
Perturbative invariant of Seifert fibered rational homology spheres associated with trivial first cohomology class.
Topology and its Applications,
Vol. 109,
Issue. 1,
p.
89.
Cochran, Tim D.
and
Melvin, Paul
2001.
Quantum cyclotomic orders of 3-manifolds.
Topology,
Vol. 40,
Issue. 1,
p.
95.
Gilmer, Patrick M
Kania-Bartoszynska, Joanna
and
Przytycki, Jozef H
2002.
3–manifold invariants and periodicity of homology spheres.
Algebraic & Geometric Topology,
Vol. 2,
Issue. 2,
p.
825.
Kerler, Thomas
2002.
p–Modular TQFT's, Milnor torsion and the Casson–Lescop invariant.
p.
119.
Le, Thang T.Q.
2003.
Quantum invariants of 3-manifolds: Integrality, splitting, and perturbative expansion.
Topology and its Applications,
Vol. 127,
Issue. 1-2,
p.
125.
Ohtsuki, Tomotada
2004.
Problems on invariants of knots and 3–manifolds.
p.
377.
Gilmer, Patrick M.
2004.
Integrality for TQFTs.
Duke Mathematical Journal,
Vol. 125,
Issue. 2,
HIKAMI, KAZUHIRO
2005.
ON THE QUANTUM INVARIANT FOR THE BRIESKORN HOMOLOGY SPHERES.
International Journal of Mathematics,
Vol. 16,
Issue. 06,
p.
661.
Lê, T.T.Q.
2006.
Encyclopedia of Mathematical Physics.
p.
348.
SATO, CHIFUMI
2006.
PERTURBATIVE INVARIANTS OF LENS SPACES ASSOCIATED WITH COHOMOLOGY CLASSES.
Journal of Knot Theory and Its Ramifications,
Vol. 15,
Issue. 07,
p.
913.
Ohtsuki, Tomotada
2007.
On the 2–loop polynomial of knots.
Geometry & Topology,
Vol. 11,
Issue. 3,
p.
1357.
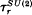 associated to q = exp(2π √ − 1/r) with r odd splits into the product of the quantum SO(3)-invariant
associated to q = exp(2π √ − 1/r) with r odd splits into the product of the quantum SO(3)-invariant 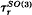 and
and 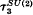 [15]. For other approaches to these invariants, see [3, 4, 5, 16, 22, 27].
[15]. For other approaches to these invariants, see [3, 4, 5, 16, 22, 27].



