Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Sørensen, Dan Erik Krarup
1996.
Accumulation theorems for quadratic polynomials.
Ergodic Theory and Dynamical Systems,
Vol. 16,
Issue. 3,
p.
555.
Ferenczi, Sébastien
and
Mauduit, Christian
1997.
Transcendence of Numbers with a Low Complexity Expansion.
Journal of Number Theory,
Vol. 67,
Issue. 2,
p.
146.
Yuan, Guocheng
and
Hunt, Brian R
1999.
Optimal orbits of hyperbolic systems.
Nonlinearity,
Vol. 12,
Issue. 4,
p.
1207.
Bullett, Shaun
and
Penrose, Christopher
1999.
Perturbing circle-packing Kleinian groups as correspondences.
Nonlinearity,
Vol. 12,
Issue. 3,
p.
635.
Sander, J.W.
and
Tijdeman, R.
2000.
The complexity of functions on lattices.
Theoretical Computer Science,
Vol. 246,
Issue. 1-2,
p.
195.
Yampolsky, Michael
and
Zakeri, Saeed
2000.
Mating Siegel quadratic polynomials.
Journal of the American Mathematical Society,
Vol. 14,
Issue. 1,
p.
25.
Jenkinson, Oliver
2000.
Frequency Locking on the Boundary of the Barycentre Set.
Experimental Mathematics,
Vol. 9,
Issue. 2,
p.
309.
Bousch, Thierry
and
Mairesse, Jean
2001.
Asymptotic height optimization for topical IFS, Tetris heaps, and the finiteness conjecture.
Journal of the American Mathematical Society,
Vol. 15,
Issue. 1,
p.
77.
BERSTEL, JEAN
2002.
RECENT RESULTS ON EXTENSIONS OF STURMIAN WORDS.
International Journal of Algebra and Computation,
Vol. 12,
Issue. 01n02,
p.
371.
Jenkinson, Oliver
and
Zamboni, Luca Q.
2004.
Characterisations of balanced words via orderings.
Theoretical Computer Science,
Vol. 310,
Issue. 1-3,
p.
247.
Jenkinson, Oliver
2005.
Maximum hitting frequency and fastest mean return time.
Nonlinearity,
Vol. 18,
Issue. 5,
p.
2305.
Blokh, Alexander
and
Oversteegen, Lex
2006.
The Julia sets of quadratic Cremer polynomials.
Topology and its Applications,
Vol. 153,
Issue. 15,
p.
3038.
Blokh, Alexander
Malaugh, James M.
Mayer, John C.
Oversteegen, Lex G.
and
Parris, Daniel K.
2006.
Rotational subsets of the circle under zd.
Topology and its Applications,
Vol. 153,
Issue. 10,
p.
1540.
Bullett, Shaun
and
Haïssinsky, Peter
2007.
Pinching holomorphic correspondences.
Conformal Geometry and Dynamics of the American Mathematical Society,
Vol. 11,
Issue. 6,
p.
65.
HARRISS, EDMUND
and
JENKINSON, OLIVER
2007.
Flattening functions on flowers.
Ergodic Theory and Dynamical Systems,
Vol. 27,
Issue. 6,
p.
1865.
BRÉMONT, JULIEN
and
SEURET, STÉPHANE
2008.
The singularity spectrum of the fish’s boundary.
Ergodic Theory and Dynamical Systems,
Vol. 28,
Issue. 1,
p.
49.
KWON, DOYONG
2008.
A devil's staircase from rotations and irrationality measures for Liouville numbers.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 145,
Issue. 3,
p.
739.
Allouche, Jean-Paul
2008.
A note on univoque self-Sturmian numbers.
RAIRO - Theoretical Informatics and Applications,
Vol. 42,
Issue. 4,
p.
659.
Levin, Genadi
2009.
Multipliers of periodic orbits of quadratic polynomials and the parameter plane.
Israel Journal of Mathematics,
Vol. 170,
Issue. 1,
p.
285.
JENKINSON, OLIVER
2009.
BALANCED WORDS AND MAJORIZATION.
Discrete Mathematics, Algorithms and Applications,
Vol. 01,
Issue. 04,
p.
463.
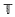 = ℝ/ℤ is ordered if and only if it is contained in a semi-circle Cμ = [μ, μ+½]. We investigate the ‘devil's staircase’ associating to each μ ε
= ℝ/ℤ is ordered if and only if it is contained in a semi-circle Cμ = [μ, μ+½]. We investigate the ‘devil's staircase’ associating to each μ ε 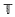 the rotation number ν of the unique minimal closed σ-invariant set contained in Cμ; we present algorithms for μ in terms of ν, and we prove (after Douady) that if ν is irrational then μ is transcendental. We apply some of this analysis to questions concerning the square root map, and mode-locking for families of circle maps, we generalize our algorithms to orbits of the shift having ‘sequences of rotation numbers’, and we conclude with a characterization of all orders of points around
the rotation number ν of the unique minimal closed σ-invariant set contained in Cμ; we present algorithms for μ in terms of ν, and we prove (after Douady) that if ν is irrational then μ is transcendental. We apply some of this analysis to questions concerning the square root map, and mode-locking for families of circle maps, we generalize our algorithms to orbits of the shift having ‘sequences of rotation numbers’, and we conclude with a characterization of all orders of points around 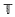 realizable by orbits of σ.
realizable by orbits of σ.



