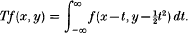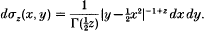Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Drury, S. W.
and
Guo, K.
1993.
Some remarks on the restriction of the Fourier transform to surfaces.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 113,
Issue. 1,
p.
153.
Travaglini, Giancarlo
1995.
Trasformate di Radon e operatori di convoluzione su gruppi e algebre di Lie.
Rendiconti del Seminario Matematico e Fisico di Milano,
Vol. 65,
Issue. 1,
p.
265.
Ferreyra, E.
Godoy, T.
and
Urciuolo, M.
2002.
The type set for some measures on $$\mathbb{R}^{2n} $$ with n-dimensional support.
Czechoslovak Mathematical Journal,
Vol. 52,
Issue. 3,
p.
575.
Oberlin, Daniel M.
2008.
Convolution Estimates and Model Surfaces of Low Codimension.
Journal of Fourier Analysis and Applications,
Vol. 14,
Issue. 3,
p.
484.
Choi, Youngwoo
2011.
Convolution estimates related to space curves.
Journal of Inequalities and Applications,
Vol. 2011,
Issue. 1,
Choi, Youngwoo
2013.
Uniform Estimates for Damped Radon Transform on the Plane.
Abstract and Applied Analysis,
Vol. 2013,
Issue. ,
p.
1.
Chung, Hyunuk
and
Ham, Seheon
2019.
Convolution estimates for measures on some complex curves.
Annali di Matematica Pura ed Applicata (1923 -),
Vol. 198,
Issue. 3,
p.
837.
Shin, Yeongtae
2019.
The L → L estimates for degenerate Radon transforms in C2.
Journal of Mathematical Analysis and Applications,
Vol. 471,
Issue. 1-2,
p.
519.
Godoy, T.
and
Rocha, P.
2023.
A decay estimate for the Fourier transform of certain singular measures in ℝ4 and applications.
Analysis Mathematica,
Vol. 49,
Issue. 2,
p.
443.
Meade, Conor
2023.
Uniform convolution estimates for complex polynomial curves in $${\mathbb {C}}^3$$.
Annali di Matematica Pura ed Applicata (1923 -),
Vol. 202,
Issue. 6,
p.
2947.
Urciuolo, Marta
and
Vallejos, Lucas
2023.
𝐿𝑝(⋅) − 𝐿𝑞(⋅) estimates for convolution operators with singular measures supported on surfaces of half the ambient dimension.
Georgian Mathematical Journal,
Vol. 30,
Issue. 3,
p.
453.