Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Lam, K. Y.
and
Yiu, P. Y. H.
1989.
Geometry of normed bilinear maps and the 16-square problem.
Mathematische Annalen,
Vol. 284,
Issue. 3,
p.
437.
Tang, Zizhou
1989.
Harmonic polynomial morphisms between Euclidean spaces.
Science in China Series A: Mathematics,
Vol. 42,
Issue. 6,
p.
570.
Scheiderer, Claus
1992.
Real Algebraic Geometry.
Vol. 1524,
Issue. ,
p.
75.
Alarcon, Ignacio
and
Yiu, Paul
1993.
Compositions of hermitian forms.
Linear and Multilinear Algebra,
Vol. 36,
Issue. 2,
p.
141.
Yiu, Paul
1994.
Deformations of Mathematical Structures II.
p.
7.
Yiu, Paul
1994.
Quadratic forms between euclidean spheres.
Manuscripta Mathematica,
Vol. 83,
Issue. 1,
p.
171.
Eells, James
and
Yiu, Paul
1995.
Polynomial harmonic morphisms between Euclidean spheres.
Proceedings of the American Mathematical Society,
Vol. 123,
Issue. 9,
p.
2921.
2000.
Compositions of Quadratic Forms.
p.
381.
TANG, ZIZHOU
2001.
NEW CONSTRUCTIONS OF EIGENMAPS BETWEEN SPHERES.
International Journal of Mathematics,
Vol. 12,
Issue. 03,
p.
277.
Тиморин, Владлен Анатольевич
Timorin, Vladlen Anatol'evich
Тиморин, Владлен Анатольевич
and
Timorin, Vladlen Anatol'evich
2004.
Окружности и алгебры Клиффорда.
Функциональный анализ и его приложения,
Vol. 38,
Issue. 1,
p.
56.
Timorin, Vladlen
2005.
Circles and Quadratic Maps Between Spheres.
Geometriae Dedicata,
Vol. 115,
Issue. 1,
p.
19.
Rodríguez-Ordóñez, Hugo
2007.
A note on the fundamental theorem of algebra for the octonions.
Expositiones Mathematicae,
Vol. 25,
Issue. 4,
p.
355.
Wu, Faen
Xiong, Yueshan
and
Zhao, Xinnuan
2015.
Classification of Quadratic Harmonic Maps of $$S^{7}$$ S 7 into $$S^{7}$$ S 7.
The Journal of Geometric Analysis,
Vol. 25,
Issue. 3,
p.
1992.
Ambrosie, Rareş
Oniciuc, Cezar
and
Ou, Ye-Lin
2023.
Biharmonic Homogeneous Polynomial Maps Between Spheres.
Results in Mathematics,
Vol. 78,
Issue. 4,




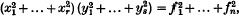
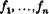 are bilinear forms with real coefficients in
are bilinear forms with real coefficients in 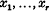 and
and 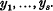 . Such an
. Such an 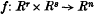 satisfying
satisfying 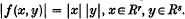 . We shall, therefore, speak of sums of squares formulae and normed bilinear maps interchangeably.
. We shall, therefore, speak of sums of squares formulae and normed bilinear maps interchangeably.