Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kempken, Gisela
1983.
Induced Conjugacy Classes in Classical Lie-Algebras.
Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg,
Vol. 53,
Issue. 1,
p.
53.
Holt, D. F.
and
Spaltenstein, N.
1985.
Nilpotent orbits of exceptional Lie algebras over algebraically closed fields of bad characteristic.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 38,
Issue. 3,
p.
330.
Borho, W.
and
Brylinski, J. -L.
1985.
Differential operators on homogeneous spaces. III.
Inventiones Mathematicae,
Vol. 80,
Issue. 1,
p.
1.
Borho, Walter
Brylinski, Jean-Luc
and
MacPherson, Robert
1987.
Springer's Weyl group representations through characteristic classes of cone bundles.
Mathematische Annalen,
Vol. 278,
Issue. 1-4,
p.
273.
Kostrikin, A. I.
and
Chubarov, I. A.
1988.
Representations of finite groups.
Journal of Soviet Mathematics,
Vol. 40,
Issue. 3,
p.
331.
Tanisaki, Toshiyuki
1988.
Representations of Lie Groups, Kyoto, Hiroshima, 1986.
p.
1.
Lehrer, G. I.
and
Shoji, T.
1990.
On flag varieties, hyperplane complements and Springer representations of Weyl groups.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 49,
Issue. 3,
p.
449.
Spaltenstein, N.
1991.
On the reflection representation in Springer's theory.
Commentarii Mathematici Helvetici,
Vol. 66,
Issue. 1,
p.
618.
Sommers, Eric
and
Trapa, Peter
1997.
The adjoint representation in rings of functions.
Representation Theory of the American Mathematical Society,
Vol. 1,
Issue. 9,
p.
182.
Sommers, E.
1997.
A family of affine Weyl group representations.
Transformation Groups,
Vol. 2,
Issue. 4,
p.
375.
Douglass, J. Matthew
1998.
Irreducible Components of Fixed Point Subvarieties of Flag Varieties.
Mathematische Nachrichten,
Vol. 189,
Issue. 1,
p.
107.
Casselman, Bill
2000.
Verifying Kottwitz’ conjecture by computer.
Representation Theory of the American Mathematical Society,
Vol. 4,
Issue. 3,
p.
32.
Aubert, Anne-Marie
2003.
Character sheaves and generalized Springer correspondence.
Nagoya Mathematical Journal,
Vol. 170,
Issue. ,
p.
47.
Jantzen, Jens Carsten
2004.
Lie Theory.
p.
1.
Fu, Baohua
2007.
Extremal contractions, stratified Mukai flops and Springer maps.
Advances in Mathematics,
Vol. 213,
Issue. 1,
p.
165.
Shoji, Toshiaki
2007.
A variant of the induction theorem for Springer representations.
Journal of Algebra,
Vol. 311,
Issue. 1,
p.
130.
Treumann, David
2009.
A topological approach to induction theorems in Springer theory.
Representation Theory of the American Mathematical Society,
Vol. 13,
Issue. 2,
p.
8.
Lusztig, G.
2009.
Unipotent classes and special Weyl group representations.
Journal of Algebra,
Vol. 321,
Issue. 11,
p.
3418.
Fu, Baohua
2010.
On Q-factorial terminalizations of nilpotent orbits.
Journal de Mathématiques Pures et Appliquées,
Vol. 93,
Issue. 6,
p.
623.
Lusztig, George
2014.
Families and Springer’s correspondence.
Pacific Journal of Mathematics,
Vol. 267,
Issue. 2,
p.
431.
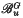 of Borel subgroups containing u, where β(u) = dim
of Borel subgroups containing u, where β(u) = dim 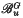 . For example, when u = 1, ρu is the sign representation of W. The map u → ρu defines an injective map from the set of unipotent conjugacy classes in G to the set of irreducible representations of W (up to isomorphism). Our purpose is to describe this map in the case where G is simple of type Eu (n = 6, 7, 8). (When G is classical or of type F4, this map is described by Shoji (9), (10); the case where G is of type G2 is contained in (11).
. For example, when u = 1, ρu is the sign representation of W. The map u → ρu defines an injective map from the set of unipotent conjugacy classes in G to the set of irreducible representations of W (up to isomorphism). Our purpose is to describe this map in the case where G is simple of type Eu (n = 6, 7, 8). (When G is classical or of type F4, this map is described by Shoji (9), (10); the case where G is of type G2 is contained in (11).



