Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Singerman, David
1980.
Symmetries and pseudo-symmetries of hyperelliptic surfaces.
Glasgow Mathematical Journal,
Vol. 21,
Issue. 1,
p.
39.
Bujalance, Emilio
1981.
Normal subgroups of N.E.C. groups.
Mathematische Zeitschrift,
Vol. 178,
Issue. 3,
p.
331.
Baskan, T.
and
Macbeath, A. M.
1982.
Centralizers of reflections in crystallographic groups.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 92,
Issue. 1,
p.
79.
Etayo Gordejuela, J. J.
1984.
Klein surfaces with maximal symmetry and their groups of automorphisms.
Mathematische Annalen,
Vol. 268,
Issue. 4,
p.
533.
Bujalance, E.
and
Gamboa, J. M.
1984.
Automorphism groups of algebraic curves ofR n of genus 2.
Archiv der Mathematik,
Vol. 42,
Issue. 3,
p.
229.
Bujalance, E.
1985.
On the structure of the automorphism group of a compact Klein surface withN boundary components (1?N?4).
Mathematische Annalen,
Vol. 270,
Issue. 1,
p.
29.
Etayo Gordejuela, J. J.
1985.
Non-orientable automorphisms of Riemann surfaces.
Archiv der Mathematik,
Vol. 45,
Issue. 4,
p.
374.
Gordejuela, J. J. Etayo
1985.
On the order of automorphism groups of Klein surfaces.
Glasgow Mathematical Journal,
Vol. 26,
Issue. 1,
p.
75.
Bujalance, Emilio
1986.
Automorphism groups of compact planar Klein surfaces.
Manuscripta Mathematica,
Vol. 56,
Issue. 1,
p.
105.
Martinez, Ernesto
1986.
Convex fundamental regions for N. E. C. groups.
Archiv der Mathematik,
Vol. 47,
Issue. 5,
p.
457.
Bujalance, J. A.
1987.
Normal subgroups of even index in an NEC group.
Archiv der Mathematik,
Vol. 49,
Issue. 6,
p.
470.
Bujalance, J. A.
1988.
Topological types of Klein surfaces with a maximum order automorphism.
Glasgow Mathematical Journal,
Vol. 30,
Issue. 1,
p.
87.
Etayo, J. J.
and
Martínez, E.
1988.
Hyperbolic polygons and NEC groups.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 104,
Issue. 2,
p.
261.
Bujalance, E
and
Etayo, J. J
1988.
A characterization of q-hyperelliptic compact planar klein surfaces.
Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg,
Vol. 58,
Issue. 1,
p.
95.
Bujalance, Emilio
Bujalance, J. A.
Gromadzki, G.
and
Martinez, E.
1989.
Groups — Korea 1988.
Vol. 1398,
Issue. ,
p.
43.
Bujalance, J. A.
1989.
Hyperelliptic compact nonorientable Klein surfaces without boundary.
Kodai Mathematical Journal,
Vol. 12,
Issue. 1,
Bujalance, Emilio
Costa, Antonio F.
and
Gamboa, J. M.
1990.
Real Analytic and Algebraic Geometry.
Vol. 1420,
Issue. ,
p.
81.
May, Coy L.
1991.
Complex doubles of bordered Klein surfaces with maximal symmetry.
Glasgow Mathematical Journal,
Vol. 33,
Issue. 1,
p.
61.
Bujalance, E.
Costa, A. F.
Natanzon, S. M.
and
Singerman, D.
1992.
Involutions of compact Klein surfaces.
Mathematische Zeitschrift,
Vol. 211,
Issue. 1,
p.
461.
May, Coy L.
1993.
Finite Groups Acting on Bordered Surfaces and the Real Genus of a Group.
Rocky Mountain Journal of Mathematics,
Vol. 23,
Issue. 2,




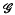 denote the group of transformations of the upper-half complex plane
denote the group of transformations of the upper-half complex plane 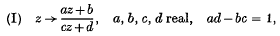
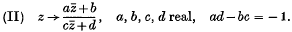
 .
.