Homeomorphisms of non-orientable two-manifolds
Published online by Cambridge University Press: 24 October 2008
Extract
In an earlier paper (1) the idea of a c-homeomorphism on a 2-manifold was introduced; it can be described in the following way. Let the 2-manifold M contain an annulus, A, one of the boundary components of which is a simple closed curve c. There is a homeomorphism of A to itself, fixed on the boundary of A, which sends radial arcs onto arcs which spiral once around A (see Fig. 1). This can be extended to
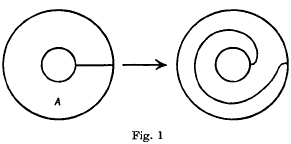
a homeomorphism of M to itself, by the identity on M — A. Intuitively this homeomorphism can be thought of as the process of cutting M along c, twisting one of the now free ends, and then glueing together again. The c-homeomorphism has, in fact, only been defined up to isotopy, but as we shall only be considering homeomorphisms up to isotopy, this is sufficient. It was shown in (1) that any orientation preserving homeomorphism of a closed orientable 2-manifold can be expressed as a product of c-homeomorphisms. In that case, a c-homeomorphism could be associated with any simple closed path on such a manifold, but on a non-orientable 2-manifold a c-homeomorphism can only be associated with a simple closed orientation preserving path. It is this fact that invalidates many of the lemmas of (1) if they are regarded as applying to the non-orientable case. The purpose of this paper is to show that (Theorem 1) c-homeomorphisms do not generate the group of all homeomorphisms of a closed nonorientable 2-manifold, but that if another elementary type of homeomorphism, the Y-homeomorphism, is introduced, then c- and Y-homeomorphisms together do generate this group (Theorem 2). This result leads to a discussion of non-orientable 3-manifolds, to a result analogous to that obtained for orientable 3-manifolds in (1), and to a new proof of the fact that any 3-manifold bounds a 4-manifold. Throughout this paper all manifolds will be considered as possessing an underlying combinatorial structure, all paths will be polygonal with respect to some subdivision of the manifold containing them, and all homeomorphisms and isotopies will be piecewise linear.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 59 , Issue 2 , April 1963 , pp. 307 - 317
- Copyright
- Copyright © Cambridge Philosophical Society 1963
References
REFERENCES
- 85
- Cited by




