Article contents
An extension of the method of steepest descents
Published online by Cambridge University Press: 24 October 2008
Abstract
In the integral
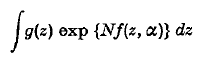
the functions g(z), f(z, α) are analytic functions of their arguments, and N is a large positive parameter. When N tends to ∞, asymptotic expansions can usually be found by the method of steepest descents, which shows that the principal contributions arise from the saddle points, i.e. the values of z at which ∂f/∂z = 0. The position of the saddle points varies with α, and if for some a (say α = 0) two saddle points coincide (say at z = 0) the ordinary method of steepest descents gives expansions which are not uniformly valid for small α. In the present paper we consider this case of two nearly coincident saddle points and construct uniform expansions as follows. A new complex variable u is introduced by the implicit relation
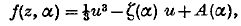
where the parameters ζ(α), A(α) are determined explicitly from the condition that the (u, z) transformation is uniformly regular near z = 0, α = 0 (see § 2 below). We show that with these values of the parameters there is one branch of the transformation which is uniformly regular. By taking u on this branch as a new variable of integration we obtain for the integral uniformly asymptotic expansions of the form
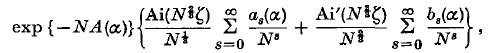
where Ai and Ai′ are the Airy function and its derivative respectively, and A(α), ζ(α) are the parameters in the transformation. The application to Bessel functions of large order is briefly described.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 53 , Issue 3 , July 1957 , pp. 599 - 611
- Copyright
- Copyright © Cambridge Philosophical Society 1957
References
REFERENCES
- 390
- Cited by




