Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Jiang, Dihua
Nien, Chufeng
and
Qin, Yujun
2008.
Local Shalika models and functoriality.
manuscripta mathematica,
Vol. 127,
Issue. 2,
p.
187.
Yang, Jae-Hyun
2009.
Langlands Functoriality Conjecture.
Kyungpook mathematical journal,
Vol. 49,
Issue. 2,
p.
355.
Khare, Chandrashekhar
Larsen, Michael
and
Savin, Gordan
2010.
Functoriality and the Inverse Galois problem II: groups of type B n and G 2 .
Annales de la Faculté des sciences de Toulouse : Mathématiques,
Vol. 19,
Issue. 1,
p.
37.
Larsen, Michael
2010.
Exponential generation and largeness for compactp-adic Lie groups.
Algebra & Number Theory,
Vol. 4,
Issue. 8,
p.
1029.
Arias-de-Reyna, S.
and
Vila, N.
2010.
Tame Galois Realizations of over.
International Mathematics Research Notices,
Hales, Thomas C.
2014.
Turing's Legacy.
p.
253.
Soudry, David
and
Tanay, Yaacov
2015.
On local descent for unitary groups.
Journal of Number Theory,
Vol. 146,
Issue. ,
p.
557.
Arias-de-Reyna, Sara
Dieulefait, Luis V.
Shin, Sug Woo
and
Wiese, Gabor
2015.
Compatible systems of symplectic Galois representations and the inverse Galois problem III. Automorphic construction of compatible systems with suitable local properties.
Mathematische Annalen,
Vol. 361,
Issue. 3-4,
p.
909.
Arias-de-Reyna, Sara
Armana, Cécile
Karemaker, Valentijn
Rebolledo, Marusia
Thomas, Lara
and
Vila, Núria
2015.
Women in Numbers Europe.
Vol. 2,
Issue. ,
p.
191.
Muić, Goran
2016.
Fourier coefficients of automorphic forms and integrable discrete series.
Journal of Functional Analysis,
Vol. 270,
Issue. 10,
p.
3639.
Arias-de-Reyna, Sara
Dieulefait, Luis
and
Wiese, Gabor
2016.
Compatible systems of symplectic Galois representations and the inverse Galois problem II: Transvections and huge image.
Pacific Journal of Mathematics,
Vol. 281,
Issue. 1,
p.
1.
Guralnick, Robert M.
Lübeck, Frank
and
Yu, Jun
2016.
Rational rigidity for F4(p).
Advances in Mathematics,
Vol. 302,
Issue. ,
p.
48.
Cadoret, Anna
and
Tamagawa, Akio
2019.
On the Geometric Image of $\mathbb{F}_{\ell}$-Linear Representations of étale Fundamental Groups.
International Mathematics Research Notices,
Vol. 2019,
Issue. 9,
p.
2735.
Bary-Soroker, Lior
and
Schlank, Tomer M.
2020.
SIEVES AND THE MINIMAL RAMIFICATION PROBLEM.
Journal of the Institute of Mathematics of Jussieu,
Vol. 19,
Issue. 3,
p.
919.
Zenteno, Adrián
2020.
Automorphic Galois representations and the inverse Galois problem for certain groups of type 𝐷ₘ.
Proceedings of the American Mathematical Society,
Vol. 149,
Issue. 1,
p.
89.
Magaard, Kay
and
Savin, Gordan
2020.
Computing finite Galois groups arising from automorphic forms.
Journal of Algebra,
Vol. 561,
Issue. ,
p.
256.
Tang, Shiang
2024.
Remarks on the inverse Galois problem over function fields.
Finite Fields and Their Applications,
Vol. 93,
Issue. ,
p.
102343.




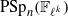 appears as a Galois group over
appears as a Galois group over 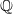 . This generalizes a result of Wiese from 2006, which inspired this paper.
. This generalizes a result of Wiese from 2006, which inspired this paper.