Article contents
 group shifts and Bernoulli factors
group shifts and Bernoulli factors
Published online by Cambridge University Press: 01 April 2008
Abstract
In this paper, a group shift is an expansive action of 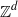 on a compact metrizable zero-dimensional group by continuous automorphisms. All group shifts factor topologically onto equal-entropy Bernoulli shifts; abelian group shifts factor by continuous group homomorphisms onto canonical equal-entropy Bernoulli group shifts; and completely positive entropy abelian group shifts are weakly algebraically equivalent to these Bernoulli factors. A completely positive entropy group (even vector) shift need not be topologically conjugate to a Bernoulli shift, and the Pinsker factor of a vector shift need not split topologically.
on a compact metrizable zero-dimensional group by continuous automorphisms. All group shifts factor topologically onto equal-entropy Bernoulli shifts; abelian group shifts factor by continuous group homomorphisms onto canonical equal-entropy Bernoulli group shifts; and completely positive entropy abelian group shifts are weakly algebraically equivalent to these Bernoulli factors. A completely positive entropy group (even vector) shift need not be topologically conjugate to a Bernoulli shift, and the Pinsker factor of a vector shift need not split topologically.
- Type
- Research Article
- Information
- Ergodic Theory and Dynamical Systems , Volume 28 , Issue 2: William Parry Memorial Volume , April 2008 , pp. 367 - 387
- Copyright
- Copyright © Cambridge University Press 2008
References
- 4
- Cited by




