Article contents
Valid Generalisation from Approximate Interpolation
Published online by Cambridge University Press: 12 September 2008
Abstract
Let 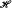 and
and 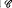 be sets of functions from domain X to ℝ. We say that
be sets of functions from domain X to ℝ. We say that 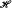 validly generalises
validly generalises 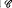 from approximate interpolation if and only if for each η > 0 and ∈, δ ∈ (0,1) there is m0(η, ∈, δ) such that for any function t ∈
from approximate interpolation if and only if for each η > 0 and ∈, δ ∈ (0,1) there is m0(η, ∈, δ) such that for any function t ∈ 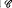 and any probability distribution
and any probability distribution  on X, if m > m0 then with
on X, if m > m0 then with  m-probability at least 1 – δ, a sample X = (x1, X2,…,xm) ∈ Xm satisfies
m-probability at least 1 – δ, a sample X = (x1, X2,…,xm) ∈ Xm satisfies
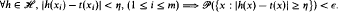
We find conditions that are necessary and sufficient for 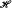 to validly generalise
to validly generalise 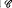 from approximate interpolation, and we obtain bounds on the sample length m0{η,∈,δ) in terms of various parameters describing the expressive power of
from approximate interpolation, and we obtain bounds on the sample length m0{η,∈,δ) in terms of various parameters describing the expressive power of 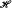 .
.
- Type
- Research Article
- Information
- Copyright
- Copyright © Cambridge University Press 1996
References
- 2
- Cited by




