Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Wright, James
2011.
From Oscillatory Integrals and Sublevel Sets to Polynomial Congruences and Character Sums.
Journal of Geometric Analysis,
Vol. 21,
Issue. 1,
p.
224.
Koh, Doowon
and
Shen, Chun-Yen
2013.
Extension and averaging operators for finite fields.
Proceedings of the Edinburgh Mathematical Society,
Vol. 56,
Issue. 2,
p.
599.
Koh, Doowon
2015.
SHARP Lp→LrESTIMATES OF RESTRICTED AVERAGING OPERATORS OVER CURVES ON PLANES IN FINITE FIELDS.
Journal of the Chungcheong Mathematical Society,
Vol. 28,
Issue. 2,
p.
251.
Koh, Doowon
Shen, Chun-Yen
and
Shparlinski, Igor
2016.
Averaging Operators Over Homogeneous Varieties Over Finite Fields.
The Journal of Geometric Analysis,
Vol. 26,
Issue. 2,
p.
1415.
Koh, Doowon
and
Yeom, Seongjun
2017.
Restriction of Averaging Operators to Algebraic Varieties over Finite Fields.
Taiwanese Journal of Mathematics,
Vol. 21,
Issue. 1,
Koh, Doowon
Shen, Chun-Yen
and
Yeom, Seongjun
2018.
Restricted averaging operators to cones over finite fields.
Forum Mathematicum,
Vol. 30,
Issue. 6,
p.
1345.
Koh, Doowon
and
Lee, Sujin
2022.
Averages and maximal averages over Product j-varieties in finite fields.
Finite Fields and Their Applications,
Vol. 79,
Issue. ,
p.
101984.
Bhowmik, Pablo
Iosevich, Alex
Koh, Doowon
and
Pham, Thang
2023.
Multi-linear forms, graphs, and -improving measures in .
Canadian Journal of Mathematics,
p.
1.




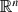 when the euclidean structure is replaced by that of a vector space over a finite field, and obtain optimal results in a number of model cases.
when the euclidean structure is replaced by that of a vector space over a finite field, and obtain optimal results in a number of model cases.