Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hattori, Shin
2009.
On a ramification bound of torsion semi-stable representations over a local field.
Journal of Number Theory,
Vol. 129,
Issue. 10,
p.
2474.
Caruso, Xavier
and
Savitt, David
2009.
Polygones de Hodge, de Newton et de l’inertie modérée des représentations semi-stables.
Mathematische Annalen,
Vol. 343,
Issue. 4,
p.
773.
Liu, Tong
2010.
A note on lattices in semi-stable representations.
Mathematische Annalen,
Vol. 346,
Issue. 1,
p.
117.
Caruso, Xavier
and
Liu, Tong
2011.
Some bounds for ramification of pn-torsion semi-stable representations.
Journal of Algebra,
Vol. 325,
Issue. 1,
p.
70.
Hattori, Shin
2012.
Ramification correspondence of finite flat group schemes over equal and mixed characteristic local fields.
Journal of Number Theory,
Vol. 132,
Issue. 10,
p.
2084.
Liu, Tong
2012.
Lattices in Filtered (φ, N)-modules.
Journal of the Institute of Mathematics of Jussieu,
Vol. 11,
Issue. 3,
p.
659.
Ozeki, Yoshiyasu
2013.
Torsion representations arising from (φ,Gˆ)-modules.
Journal of Number Theory,
Vol. 133,
Issue. 11,
p.
3810.
Caruso, Xavier
2013.
Représentations galoisiennes p-adiques et (φ,τ)-modules.
Duke Mathematical Journal,
Vol. 162,
Issue. 13,
Emerton, Matthew
Gee, Toby
and
Herzig, Florian
2013.
Weight cycling and Serre-type conjectures for unitary groups.
Duke Mathematical Journal,
Vol. 162,
Issue. 9,
Maulik, Davesh
2014.
Supersingular K3 surfaces for large primes.
Duke Mathematical Journal,
Vol. 163,
Issue. 13,
Hattori, Shin
2014.
On lower ramification subgroups and canonical subgroups.
Algebra & Number Theory,
Vol. 8,
Issue. 2,
p.
303.
Kim, Wansu
2015.
The Relative Breuil–Kisin Classification ofp-Divisible Groups and Finite Flat Group Schemes.
International Mathematics Research Notices,
Vol. 2015,
Issue. 17,
p.
8152.
Emerton, Matthew
and
Gee, Toby
2015.
p-adic Hodge-theoretic properties of étale cohomology with mod pcoefficients, and the cohomology of Shimura varieties.
Algebra & Number Theory,
Vol. 9,
Issue. 5,
p.
1035.
GEE, TOBY
LIU, TONG
and
SAVITT, DAVID
2015.
THE WEIGHT PART OF SERRE’S CONJECTURE FOR .
Forum of Mathematics, Pi,
Vol. 3,
Issue. ,
Gao, Hui
2017.
Galois lattices and strongly divisible lattices in the unipotent case.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2017,
Issue. 728,
p.
263.
Gao, Hui
2017.
Crystalline liftings and the weight part of Serre’s conjecture.
Israel Journal of Mathematics,
Vol. 221,
Issue. 1,
p.
117.
Park, Chol
2017.
Reduction modulo 𝑝 of certain semi-stable representations.
Transactions of the American Mathematical Society,
Vol. 369,
Issue. 8,
p.
5425.
Morra, Stefano
and
Park, Chol
2017.
Serre weights for three-dimensional ordinary Galois representations.
Journal of the London Mathematical Society,
Vol. 96,
Issue. 2,
p.
394.
Herzig, Florian
Le, Daniel
and
Morra, Stefano
2017.
On mod local-global compatibility for in the ordinary case.
Compositio Mathematica,
Vol. 153,
Issue. 11,
p.
2215.
Liu, Tong
2018.
Compatibility of Kisin modules for different uniformizers.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2018,
Issue. 740,
p.
1.




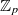 -lattices in semi-stable
-lattices in semi-stable 