Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chenevier, G.
and
Clozel, L.
2008.
Corps de nombres peu ramifiés et formes automorphes autoduales.
Journal of the American Mathematical Society,
Vol. 22,
Issue. 2,
p.
467.
Weinstein, Jared
2009.
Hilbert Modular Forms with Prescribed Ramification.
International Mathematics Research Notices,
Vol. 2009,
Issue. 8,
p.
1388.
Ivanov, Alexander
2016.
Stable sets of primes in number fields.
Algebra & Number Theory,
Vol. 10,
Issue. 1,
p.
1.




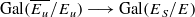 are injective. We discuss generalizations of this result.
are injective. We discuss generalizations of this result.