Hostname: page-component-8448b6f56d-sxzjt Total loading time: 0 Render date: 2024-04-23T11:45:10.263Z Has data issue: false hasContentIssue false
  • English
  • Français

Flattening functions on flowers

Published online by Cambridge University Press:  01 December 2007

EDMUND HARRISS  and
OLIVER JENKINSON
EDMUND HARRISS
Affiliation:
School of Mathematical Sciences, Queen Mary, University of London, Mile End Road, London E1 4NS, UK (email: edmund.harriss@mathematicians.org.uk, omj@maths.qmul.ac.uk)
OLIVER JENKINSON
Affiliation:
School of Mathematical Sciences, Queen Mary, University of London, Mile End Road, London E1 4NS, UK (email: edmund.harriss@mathematicians.org.uk, omj@maths.qmul.ac.uk)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let T be an orientation-preserving Lipschitz expanding map of the circle 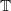. A pre-image selector is a map 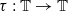with finitely many discontinuities, each of which is a jump discontinuity, and such that τ(x)∈T−1(x) for all . The closure of the image of a pre-image selector is called a flower and a flower with p connected components is called a p-flower. We say that a real-valued Lipschitz function can be Lipschitz flattened on a flower whenever it is Lipschitz cohomologous to a constant on that flower. The space of Lipschitz functions which can be flattened on a given p-flower is shown to be of codimension p in the space of all Lipschitz functions, and the linear constraints determining this subspace are derived explicitly. If a Lipschitz function f has a maximizing measure S which is Sturmian (i.e. is carried by a 1-flower), it is shown that f can be Lipschitz flattened on some 1-flower carrying S.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 27 , Issue 6 , December 2007 , pp. 1865 - 1886
Copyright
Copyright © Cambridge University Press 2007

References

[1]Anagnostopoulou, V., Díaz-Ordaz, K., Jenkinson, O. and Richard, C.. Escape from a semi-circle and Sturmian maximizing measures. Preprint, 2007.Google Scholar
[2]Bousch, T.. Le poisson n’a pas d’arêtes. Ann. Inst. H. Poincaré Probab. Statist. 36 (2000), 489–508.CrossRefGoogle Scholar
[3]Bousch, T.. La condition de Walters. Ann. Sci. École Norm. Sup. (4) 34 (2001), 287–311.CrossRefGoogle Scholar
[4]Bousch, T. and Jenkinson, O.. Cohomology classes of dynamically non-negative C k functions. Invent. Math. 148 (2002), 207–217.CrossRefGoogle Scholar
[5]Bousch, T. and Mairesse, J.. Asymptotic height optimization for topical IFS, tetris heaps, and the finiteness conjecture. J. Amer. Math. Soc. 15 (2002), 77–111.CrossRefGoogle Scholar
[6]Brémont, J.. Dynamics of injective quasi-contractions. Ergod. Th. & Dynam. Sys. 26 (2006), 19–44.CrossRefGoogle Scholar
[7]Brémont, J.. Finite flowers and maximizing measures for generic Lipschitz functions on the circle. Nonlinearity 9 (2006), 813–828.CrossRefGoogle Scholar
[8]Bullett, S. and Sentenac, P.. Ordered orbits of the shift, square roots, and the devil’s staircase. Math. Proc. Cambridge Philos. Soc. 115 (1994), 451–481.CrossRefGoogle Scholar
[9]Conze, J.-P. and Guivarc’h, Y.. Croissance des sommes ergodiques. Manuscript, circa 1993.Google Scholar
[10]Contreras, G., Lopes, A. O. and Thieullen, Ph.. Lyapunov minimizing measures for expanding maps of the circle. Ergod. Th. & Dynam. Sys. 21 (2001), 1379–1409.CrossRefGoogle Scholar
[11]Jenkinson, O.. Frequency locking on the boundary of the barycentre set. Experiment. Math. 9 (2000), 309–317.CrossRefGoogle Scholar
[12]Jenkinson, O.. Ergodic optimization. Discrete Contin. Dyn. Syst. Ser. B 15 (2006), 197–224.CrossRefGoogle Scholar
[13]Jenkinson, O.. Optimization and majorization of invariant measures. Electron. Res. Announc. Amer. Math. Soc. 13 (2007), 1–12.CrossRefGoogle Scholar
[14]Jenkinson, O.. A partial order on ×2-invariant measures. Preprint, 2006.Google Scholar
[15]Katok, A. and Hasselblatt, B.. Introduction to the Modern Theory of Dynamical Systems. Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
[16]Livšic, A.. Homology properties of Y-systems. Mat. Zametki 10 (1971), 758–763.Google Scholar
[17]Lothaire, M.. Algebraic Combinatorics on Words (Encyclopaedia of Mathematics and its Applications, 90). Cambridge University Press, Cambridge, 2002.CrossRefGoogle Scholar
[18]Morse, M. and Hedlund, G. A.. Symbolic dynamics II. Sturmian trajectories. Amer. J. Math. 62 (1940), 1–42.CrossRefGoogle Scholar
[19]Pytheas Fogg, N.. Substitutions in Dynamics, Arithmetics and Combinatorics (Lecture Notes in Mathematics, 1794). Springer, Berlin, 2002.CrossRefGoogle Scholar
[20]Ziemer, W.. Weakly Differentiable Functions. Springer, Berlin, 1989.CrossRefGoogle Scholar