Hostname: page-component-8448b6f56d-xtgtn Total loading time: 0 Render date: 2024-04-18T03:39:41.653Z Has data issue: false hasContentIssue false
  • English
  • Français

Γ-limit for the extended Fisher–Kolmogorov equation

Published online by Cambridge University Press:  12 July 2007

D. Hilhorst ,
L. A. Peletier  and
R. Schätzle
D. Hilhorst
Affiliation:
Analyse Numérique et EDP, CNRS, et Université de Paris-Sud, 91405 Orsay, France
L. A. Peletier
Affiliation:
Mathematical Institute, Leiden University, The Netherlands
R. Schätzle
Affiliation:
Departement der Mathematik, ETH Zentrum, Zürich, Switzerland
Get access Rights & Permissions [Opens in a new window]

Abstract

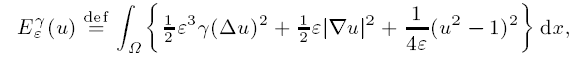
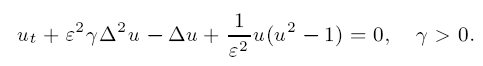
We consider the Lyapunov functional, of the rescaled Extended Fisher-Kolmogorov equation This is a fourth order generalization of the Fisher–Kolmogorov or Allen–Cahn equation. We prove that if ε → 0, then tends to the area functional in the sense of Γ-limits, where the transition energy is given by the one-dimensional kink of the Extended Fisher–Kolmogorov equation.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 132 , Issue 1 , February 2002 , pp. 141 - 162
Copyright
Copyright © Royal Society of Edinburgh 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)