Hostname: page-component-76fb5796d-2lccl Total loading time: 0 Render date: 2024-04-26T14:59:29.282Z Has data issue: false hasContentIssue false
  • English
  • Français

Tautological rings of spaces of pointed genus two curves of compact type

Part of: Families, fibrations Curves Fiber spaces and bundles Cycles and subschemes Singularities Projective and enumerative geometry

Published online by Cambridge University Press:  17 June 2016

Dan Petersen
Dan Petersen*
Affiliation:
Department of Mathematical Sciences, University of Copenhagen, Universitetsparken 5, 2100 København Ø, Denmark email danpete@math.ku.dk
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that the tautological ring of 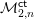${\mathcal{M}}_{2,n}^{\mathsf{ct}}$, the moduli space of $n$-pointed genus two curves of compact type, does not have Poincaré duality for any 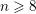$n\geqslant 8$. This result is obtained via a more general study of the cohomology groups of 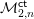${\mathcal{M}}_{2,n}^{\mathsf{ct}}$. We explain how the cohomology can be decomposed into pieces corresponding to different local systems and how the tautological cohomology can be identified within this decomposition. 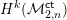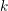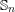Our results allow the computation of $H^{k}({\mathcal{M}}_{2,n}^{\mathsf{ct}})$ for any $k$ and $n$ considered both as $\mathbb{S}_{n}$-representation and as mixed Hodge structure/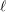$\ell$-adic Galois representation considered up to semi-simplification. A consequence of our results is also that all even cohomology of 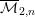$\overline{{\mathcal{M}}}_{2,n}$ is tautological for 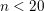$n<20$, and that the tautological ring of 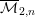$\overline{{\mathcal{M}}}_{2,n}$ fails to have Poincaré duality for all 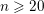$n\geqslant 20$. This improves and simplifies results of the author and Orsola Tommasi.

Keywords

tautological ringFaber conjecturesmoduli of curvesGromov–Witten theorycohomology of moduli spaces

MSC classification

Primary: 14H10: Families, moduli (algebraic) 14C17: Intersection theory, characteristic classes, intersection multiplicities 32S60: Stratifications; constructible sheaves; intersection cohomology 14N35: Gromov-Witten invariants, quantum cohomology, Gopakumar-Vafa invariants, Donaldson-Thomas invariants 14D07: Variation of Hodge structures
Secondary: 55R55: Fiberings with singularities
Type
Research Article
Information
Compositio Mathematica , Volume 152 , Issue 7 , July 2016 , pp. 1398 - 1420
Copyright
© The Author 2016 

References

Ash, A., Ginzburg, D. and Rallis, S., Vanishing periods of cusp forms over modular symbols , Math. Ann. 296 (1993), 709–723, doi:10.1007/BF01445131.Google Scholar
Beĭlinson, A. A., Bernstein, J. and Deligne, P., Faisceaux pervers , in Analysis and topology on singular spaces, I (Luminy, 1981), Astérisque, vol. 100 (Société Mathématique de France, Paris, 1982), 5–171.Google Scholar
de Cataldo, M. A. A. and Migliorini, L., The decomposition theorem, perverse sheaves and the topology of algebraic maps , Bull. Amer. Math. Soc. (N.S.) 46 (2009), 535–633, doi:10.1090/S0273-0979-09-01260-9.Google Scholar
Deligne, P., Théorie de Hodge. II , Publ. Math. Inst. Hautes Études Sci. 40 (1971), 5–57.CrossRefGoogle Scholar
Deligne, P., Théorie de Hodge. III , Publ. Math. Inst. Hautes Études Sci. 44 (1974), 5–77.CrossRefGoogle Scholar
Faber, C., A conjectural description of the tautological ring of the moduli space of curves , in Moduli of curves and abelian varieties, Aspects of Mathematics, vol. E33 (Vieweg, Braunschweig, 1999), 109–129.Google Scholar
Faber, C., Hodge integrals, tautological classes and Gromov–Witten theory , in Algebraic geometry and integrable systems related to string theory, RIMS Kôkyûroku, vol. 1232 (RIMS, Kyoto, 2001), 78–87.Google Scholar
Faber, C., Tautological algebras of moduli spaces of curves , in Moduli spaces of Riemann surfaces (American Mathematical Society, Providence, RI; Institute for Advanced Study (IAS), Princeton, NJ, 2013), 197–219.CrossRefGoogle Scholar
Faber, C. and Pandharipande, R., Relative maps and tautological classes , J. Eur. Math. Soc. (JEMS) 7 (2005), 13–49, doi:10.4171/JEMS/20.Google Scholar
Fulton, W. and MacPherson, R., A compactification of configuration spaces , Ann. of Math. (2) 139 (1994), 183–225, doi:10.2307/2946631.Google Scholar
Getzler, E., Operads and moduli spaces of genus 0 Riemann surfaces , in The moduli space of curves (Texel Island, 1994), Progress in Mathematics, vol. 129 (Birkhäuser, Boston, MA, 1995), 199–230.CrossRefGoogle Scholar
Getzler, E., Mixed Hodge structures of configuration spaces. Preprint (1995) 96-61, Max-Planck-Institut für Mathematik, Bonn; arXiv:alg-geom/9510018.Google Scholar
Getzler, E., Resolving mixed Hodge modules on configuration spaces , Duke Math. J. 96 (1999), 175–203, doi:10.1215/S0012-7094-99-09605-9.Google Scholar
Getzler, E. and Pandharipande, R., The Betti numbers of ℳ 0, n (r, d) , J. Algebraic Geom. 15 (2006), 709–732, doi:10.1090/S1056-3911-06-00425-5.Google Scholar
Ghitza, A. and McAndrew, A., Experimental evidence for Maeda’s conjecture on modular forms , Tbil. Math. J. 5 (2012), 55–69.Google Scholar
Graber, T. and Pandharipande, R., Constructions of nontautological classes on moduli spaces of curves , Michigan Math. J. 51 (2003), 93–109, doi:10.1307/mmj/1049832895.CrossRefGoogle Scholar
Hain, R. and Looijenga, E., Mapping class groups and moduli spaces of curves , in Algebraic geometry—Santa Cruz 1995, Proceedings of Symposia in Pure Mathematics, vol. 62 (American Mathematical Society, Providence, RI, 1997), 97–142.CrossRefGoogle Scholar
Harder, G., The Eisenstein motive for the cohomology of GSp2(ℤ) , in Geometry and arithmetic, EMS Series of Congress Reports, eds Faber, C., Farkas, G. and de Jong, R. (European Mathematical Society, Zürich, 2012), 143–164, doi:10.4171/119-1/10.Google Scholar
Kohnen, W., Modular forms of half-integral weight on Γ0(4) , Math. Ann. 248 (1980), 249–266, doi:10.1007/BF01420529.Google Scholar
Kohnen, W. and Zagier, D., Values of L-series of modular forms at the center of the critical strip , Invent. Math. 64 (1981), 175–198, doi:10.1007/BF01389166.CrossRefGoogle Scholar
Lang, S., Introduction to modular forms, Grundlehren der mathematischen Wissenschaften, vol. 222 (Springer, Berlin–New York, 1976).Google Scholar
Lemma, F., On higher regulators of Siegel threefolds I: The vanishing on the boundary , Asian J. Math. 19 (2015), 83–120, doi:10.4310/AJM.2015.v19.n1.a4.CrossRefGoogle Scholar
Looijenga, E. and Rapoport, M., Weights in the local cohomology of a Baily–Borel compactification , in Complex geometry and Lie theory (Sundance, UT, 1989), Proceedings of Symposia in Pure Mathematics, vol. 53 (American Mathematical Society, Providence, RI, 1991), 223–260; doi:10.1090/pspum/053/1141203.Google Scholar
Pandharipande, R., Three questions in Gromov–Witten theory , in Proceedings of the international congress of mathematicians, vol. II (Beijing, 2002) (Higher Education Press, Beijing, 2002), 503–512.Google Scholar
Petersen, D., Cohomology of local systems on loci of d-elliptic abelian surfaces , Michigan Math. J. 62 (2013), 705–720, doi:10.1307/mmj/1387226161.Google Scholar
Petersen, D., The structure of the tautological ring in genus one , Duke Math. J. 163 (2014), 777–793, doi:10.1215/00127094-2429916.Google Scholar
Petersen, D., Cohomology of local systems on the moduli of principally polarized abelian surfaces , Pacific J. Math. 275 (2015), 39–61, doi:10.2140/pjm.2015.275.39.Google Scholar
Petersen, D. and Tommasi, O., The Gorenstein conjecture fails for the tautological ring of M 2, n , Invent. Math. 196 (2014), 139–161.Google Scholar
Pink, R., On l-adic sheaves on Shimura varieties and their higher direct images in the Baily–Borel compactification , Math. Ann. 292 (1992), 197–240, doi:10.1007/BF01444618.Google Scholar
Pixton, A., The tautological ring of the moduli space of curves, PhD thesis, Princeton University (2013).Google Scholar
Qiu, Y., Tate classes on Siegel 3-folds. Preprint (2014), http://math.columbia.edu/∼qiu/.Google Scholar
Saito, M., Introduction to mixed Hodge modules , in Actes du colloque de théorie de Hodge (Luminy, 1987), Astérisque, vol. 179–180 (Société Mathématique de France, 1989), 10, 145–162.Google Scholar
Saito, M., Mixed Hodge modules , Publ. Res. Inst. Math. Sci. 26 (1990), 221–333, doi:10.2977/prims/1195171082.Google Scholar
Schwermer, J., On Euler products and residual Eisenstein cohomology classes for Siegel modular varieties , Forum Math. 7 (1995), 1–28, doi:10.1515/form.1995.7.1.Google Scholar
Yin, Q., Cycles on curves and Jacobians: a tale of two tautological rings , Algebraic Geom. 3 (2016), 179–210, doi:10.14231/AG-2016-009.Google Scholar
Zucker, S., Hodge theory with degenerating coefficients. L 2 cohomology in the Poincaré metric , Ann. of Math. (2) 109 (1979), 415–476, doi:10.2307/1971221.Google Scholar