Hostname: page-component-76fb5796d-45l2p Total loading time: 0 Render date: 2024-04-25T10:46:39.129Z Has data issue: false hasContentIssue false
  • English
  • Français

Relatively weakly mixing models for dynamical systems

Published online by Cambridge University Press:  10 November 2014

ZHENGXING LIAN  and
SONG SHAO
ZHENGXING LIAN
Affiliation:
Department of Mathematics, University of Science and Technology of China, Hefei, Anhui 230026, PR China email lianzx@mail.ustc.edu.cn, songshao@ustc.edu.cn
SONG SHAO
Affiliation:
Department of Mathematics, University of Science and Technology of China, Hefei, Anhui 230026, PR China email lianzx@mail.ustc.edu.cn, songshao@ustc.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

A classical result in ergodic theory says that there always exists a topological model for any factor map 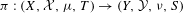${\it\pi}:(X,{\mathcal{X}},{\it\mu},T)\rightarrow (Y,{\mathcal{Y}},{\it\nu},S)$ of ergodic systems. That is, there are some topological factor map 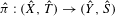$\hat{{\it\pi}}:(\hat{X},\hat{T})\rightarrow ({\hat{Y}},{\hat{S}})$ and invariant measures $\hat{{\it\mu}}$, $\hat{{\it\nu}}$ such that the diagram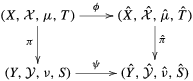

$$\begin{eqnarray}\displaystyle & & \displaystyle \nonumber\end{eqnarray}$$
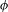is commutative, where ${\it\phi}$ and 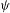${\it\psi}$ are measure theoretical isomorphisms. In this paper, we show that one can require that in the above result 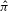$\hat{{\it\pi}}$ is either weakly mixing or finite-to-one. Also, we present some related questions.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 4 , June 2016 , pp. 1204 - 1220
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Béguin, F., Crovisier, S. and Le Roux, F.. Realisation of measured dynamics as uniquely ergodic minimal homeomorphisms on manifolds. Math. Z. 270 (2012), 59–102.Google Scholar
Ellis, R., Glasner, S. and Shapiro, L. P.. Proximal-isometric flows. Adv. Math. 17(3) (1975), 213–260.CrossRefGoogle Scholar
Furstenberg, H.. Recurrence in Ergodic Theory and Combinatorial Number Theory (M. B. Porter Lectures). Princeton University Press, Princeton, NJ, 1981.Google Scholar
Furstenberg, H. and Weiss, B.. On almost 1–1 extensions. Israel J. Math. 65(3) (1989), 311–322.Google Scholar
Glasner, E.. Ergodic Theory via Joinings (Mathematical Surveys and Monographs, 101). American Mathematical Society, Providence, RI, 2003.Google Scholar
Glasner, E.. Topological weak mixing and quasi-Bohr systems. Israel J. Math. 148 (2005), 277–304.Google Scholar
Glasner, S. and Weiss, B.. On the construction of minimal skew products. Israel J. Math. 34(4) (1979), 321–336.Google Scholar
Glasner, E. and Weiss, B.. On the interplay between measurable and topological dynamics. Handbook of Dynamical Systems. Vol. 1B. Elsevier, Amsterdam, 2006, pp. 597–648.Google Scholar
Jewett, R. I.. The prevalence of uniquely ergodic systems. J. Math. Mech. 19 (1969–1970), 717–729.Google Scholar
Krieger, W.. On unique ergodicity. Proceedings of the Sixth Berkeley Symposium on Mathematical Statistics and Probability (University of California, Berkeley, CA, 1970–1971), Probability Theory. Vol. II. University of California Press, Berkeley, CA, 1972, pp. 327–346.Google Scholar
Lehrer, E.. Topological mixing and uniquely ergodic systems. Israel J. Math. 57(2) (1987), 239–255.Google Scholar
Lindenstrauss, E.. Measurable distal and topological distal systems. Ergod. Th. & Dynam. Sys. 19 (1999), 1063–1076.Google Scholar
McMahon, D. C.. Weak mixing and a note on a structure theorem for minimal transformation groups. Illinois J. Math. 20(2) (1976), 186–197.Google Scholar
Rohlin, V. A.. On the fundamental ideas of measure theory. Mat. Sb. 25(67)(1) (1949), 107–150; Engl. transl. Amer. Math. Soc. Transl. Ser. 1 10 (1962), 1–54.Google Scholar
Rosenthal, A.. On strictly ergodic models for commuting ergodic transformations. Ann. Inst. Henri Poincaré Probab. Stat. 25(1) (1989), 73–92.Google Scholar
Veech, W. A.. Topological dynamics. Bull. Amer. Math. Soc. 83 (1977), 775–830.Google Scholar
Weiss, B.. Strictly ergodic models for dynamical systems. Bull. Amer. Math. Soc. 13(2) (1985), 143–146.Google Scholar
Weiss, B.. Single Orbit Dynamics (Regional Conference Series in Mathematics, 95). American Mathematical Society, Providence, RI, 2000.Google Scholar