Hostname: page-component-76fb5796d-2lccl Total loading time: 0 Render date: 2024-04-25T21:13:33.772Z Has data issue: false hasContentIssue false
  • English
  • Français

OPTIMISTIC LIMITS OF THE COLORED JONES POLYNOMIALS AND THE COMPLEX VOLUMES OF HYPERBOLIC LINKS

Part of: Partial differential equations on manifolds; differential operators Real and complex geometry Low-dimensional topology

Published online by Cambridge University Press:  14 March 2016

JINSEOK CHO
JINSEOK CHO*
Affiliation:
Pohang Mathematics Institute, POSTECH, Gyungbuk 37673, Republic of Korea email dol0425@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The optimistic limit is a mathematical formulation of the classical limit, which is a physical method to estimate the actual limit by using the saddle-point method of a certain potential function. The original optimistic limit of the Kashaev invariant was formulated by Yokota, and a modified formulation was suggested by the author and others. This modified version is easier to handle and more combinatorial than the original one. On the other hand, it is known that the Kashaev invariant coincides with the evaluation of the colored Jones polynomial at a certain root of unity. This optimistic limit of the colored Jones polynomial was also formulated by the author and others, but it is very complicated and needs many unnatural assumptions. In this article, we suggest a modified optimistic limit of the colored Jones polynomial, following the idea of the modified optimistic limit of the Kashaev invariant, and show that it determines the complex volume of a hyperbolic link. Furthermore, we show that this optimistic limit coincides with the optimistic limit of the Kashaev invariant modulo 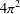$4{\it\pi}^{2}$. This new version is easier to handle and more combinatorial than the old version, and has many advantages over the modified optimistic limit of the Kashaev invariant. Because of these advantages, several applications have already appeared and more are in preparation.

Keywords

volume conjectureoptimistic limitcolored Jones polynominalcomplex volume

MSC classification

Primary: 57M27: Invariants of knots and 3-manifolds
Secondary: 51M25: Length, area and volume 58J28: Eta-invariants, Chern-Simons invariants
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 100 , Issue 3 , June 2016 , pp. 303 - 337
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Cho, J., ‘Optimistic limit of the colored Jones polynomial and the existence of a solution’, Proc. Amer. Math. Soc. 144 (2016), 1803–1814.CrossRefGoogle Scholar
Cho, J., Quandle theory and optimistic limits of representations of knot groups. Preprint, 2014,arXiv:1409.1764.Google Scholar
Cho, J., ‘Connected sum of representations of knot groups’, J. Knot Theory Ramifications 3(24) (2015), 1550020 (18 pages).Google Scholar
Cho, J., Kim, H. and Kim, S., ‘Optimistic limits of Kashaev invariants and complex volumes of hyperbolic links’, J. Knot Theory Ramifications 10(23) (2014), 1450049 (32 pages).Google Scholar
Cho, J. and Murakami, J., ‘The complex volumes of twist knots via colored Jones polynomials’, J. Knot Theory Ramifications 11(19) (2010), 1401–1421.CrossRefGoogle Scholar
Cho, J. and Murakami, J., ‘Optimistic limits of the colored Jones polynomials’, J. Korean Math. Soc. 3(50) (2013), 641–693.CrossRefGoogle Scholar
Cho, J. and Murakami, J., Reidemeister transformations of the potential function and the solution. Preprint, 2015, arXiv:1509.02378.Google Scholar
Cho, J., Murakami, J. and Yokota, Y., ‘The complex volumes of twist knots’, Proc. Amer. Math. Soc. 10(137) (2009), 3533–3541.CrossRefGoogle Scholar
Hikami, K., ‘Generalized volume conjecture and the A-polynomials: the Neumann–Zagier potential function as a classical limit of the partition function’, J. Geom. Phys. 9(57) (2007), 1895–1940.CrossRefGoogle Scholar
Hikami, K. and Inoue, R., ‘Braids, complex volume and cluster algebras’, Algebr. Geom. Topol. 4(15) (2015), 2175–2194.CrossRefGoogle Scholar
Kashaev, R. M., ‘The hyperbolic volume of knots from the quantum dilogarithm’, Lett. Math. Phys. 3(39) (1997), 269–275.CrossRefGoogle Scholar
Luo, F., Tillmann, S. and Yang, T., ‘Thurston’s spinning construction and solutions to the hyperbolic gluing equations for closed hyperbolic 3-manifolds’, Proc. Amer. Math. Soc. 1(141) (2013), 335–350.Google Scholar
McMullen, C. T., ‘The evolution of geometric structures on 3-manifolds’, Bull. Amer. Math. Soc. (N.S.) 2(48) (2011), 259–274.CrossRefGoogle Scholar
Murakami, H., ‘Optimistic calculations about the Witten–Reshetikhin–Turaev invariants of closed three-manifolds obtained from the figure-eight knot by integral Dehn surgeries’, Sūrikaisekikenkyūsho Kōkyūroku, Recent Progress Towards the Volume Conjecture, Kyoto, 2000, 70–79 (in Japanese).Google Scholar
Murakami, H. and Murakami, J., ‘The colored Jones polynomials and the simplicial volume of a knot’, Acta Math. 1(186) (2001), 85–104.CrossRefGoogle Scholar
Murakami, H., Murakami, J., Okamoto, M., Takata, T. and Yokota, Y., ‘Kashaev’s conjecture and the Chern–Simons invariants of knots and links’, Experiment. Math. 3(11) (2002), 427–435.CrossRefGoogle Scholar
Ohnuki, K., ‘The colored Jones polynomials of 2-bridge link and hyperbolicity equations of its complements’, J. Knot Theory Ramifications 6(14) (2005), 751–771.CrossRefGoogle Scholar
Segerman, H. and Tillmann, S., ‘Pseudo-developing maps for ideal triangulations I: essential edges and generalised hyperbolic gluing equations’, in: Topology and Geometry in Dimension Three, Contemporary Mathematics, 560 (American Mathematical Society, Providence, RI, 2011), 85–102.CrossRefGoogle Scholar
Yokota, Y., ‘On the complex volume of hyperbolic knots’, J. Knot Theory Ramifications 7(20) (2011), 955–976.CrossRefGoogle Scholar
Yokota, Y., On the volume conjecture for hyperbolic knots. Preprint, 2000, arXiv:0009165.Google Scholar
Zickert, C. K., ‘The volume and Chern–Simons invariant of a representation’, Duke Math. J. 3(150) (2009), 489–532.Google Scholar