Hostname: page-component-76fb5796d-zzh7m Total loading time: 0 Render date: 2024-04-26T11:15:02.878Z Has data issue: false hasContentIssue false
  • English
  • Français

Direct numerical simulation of Taylor–Couette flow with grooved walls: torque scaling and flow structure

Published online by Cambridge University Press:  06 April 2016

Xiaojue Zhu ,
Rodolfo Ostilla-Mónico ,
Roberto Verzicco  and
Detlef Lohse
Xiaojue Zhu*
Affiliation:
Physics of Fluids Group, MESA+ Institute and J. M. Burgers Centre for Fluid Dynamics, University of Twente, P.O. Box 217, 7500AE Enschede, The Netherlands
Rodolfo Ostilla-Mónico
Affiliation:
Physics of Fluids Group, MESA+ Institute and J. M. Burgers Centre for Fluid Dynamics, University of Twente, P.O. Box 217, 7500AE Enschede, The Netherlands
Roberto Verzicco
Affiliation:
Physics of Fluids Group, MESA+ Institute and J. M. Burgers Centre for Fluid Dynamics, University of Twente, P.O. Box 217, 7500AE Enschede, The Netherlands Dipartimento di Ingegneria Industriale, University of Rome ‘Tor Vergata’, Via del Politecnico 1, Roma 00133, Italy
Detlef Lohse
Affiliation:
Physics of Fluids Group, MESA+ Institute and J. M. Burgers Centre for Fluid Dynamics, University of Twente, P.O. Box 217, 7500AE Enschede, The Netherlands Max-Planck Institute for Dynamics and Self-Organization, 37077 Göttingen, Germany
*
†Email address for correspondence: xiaojue.zhu@utwente.nl
Get access Rights & Permissions [Opens in a new window]

Abstract

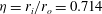We present direct numerical simulations of Taylor–Couette flow with grooved walls at a fixed radius ratio ${\it\eta}=r_{i}/r_{o}=0.714$ with inner cylinder Reynolds number up to 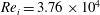$Re_{i}=3.76\times 10^{4}$, corresponding to Taylor number up to 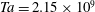$Ta=2.15\times 10^{9}$. The grooves are axisymmetric V-shaped obstacles attached to the wall with a tip angle of 90°. Results are compared to the smooth wall case in order to investigate the effects of grooves on Taylor–Couette flow. We focus on the effective scaling laws for the torque, flow structures, and boundary layers. It is found that, when the groove height is smaller than the boundary layer thickness, the torque is the same as that of the smooth wall cases. With increasing 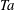$Ta$, the boundary layer thickness becomes smaller than the groove height. Plumes are ejected from the tips of the grooves and secondary circulations between the latter are formed. This is associated with a sharp increase of the torque, and thus the effective scaling law for the torque versus 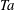$Ta$ becomes much steeper. Further increasing 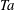$Ta$ does not result in an additional slope increase. Instead, the effective scaling law saturates to the ‘ultimate’ regime effective exponents seen for smooth walls. It is found that even though after saturation the slope is the same as for the smooth wall case, the absolute value of torque is increased, and more so with the larger size of the grooves.

JFM classification

Convection: Plumes/thermals Turbulent Flows: Turbulence simulation
Type
Papers
Information
Journal of Fluid Mechanics , Volume 794 , 10 May 2016 , pp. 746 - 774
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.CrossRefGoogle Scholar
van den Berg, T., Doering, C., Lohse, D. & Lathrop, D. 2003 Smooth and rough boundaries in turbulent Taylor–Couette flow. Phys. Rev. E 68, 036307.Google ScholarPubMed
Brauckmann, H. J. & Eckhardt, B. 2013 Direct numerical simulations of local and global torque in Taylor–Couette flow up to $Re=30\,000$ . J. Fluid Mech. 718, 398–427.Google Scholar
Cadot, O., Couder, Y., Daerr, A., Douady, S. & Tsinober, A. 1997 Energy injection in closed turbulent flows: stirring through boundary layers versus inertial stirring. Phys. Rev. E 56, 427–433.Google Scholar
Choi, H., Moin, P. & Kim, J. 1993 Direct numerical simulation of turbulent flow over riblets. J. Fluid Mech. 255, 503–539.Google Scholar
Chu, D. C. & Karniadakis, G. E. 1993 Adirect numerical simulation of laminar and turbulent flow over riblet-mounted surfaces. J. Fluid Mech. 250, 1–42.CrossRefGoogle Scholar
Ciliberto, S. & Laroche, C. 1999 Random roughness of boundary increases the turbulent scaling exponents. Phys. Rev. Lett. 82, 3998–4001.CrossRefGoogle Scholar
Du, Y.-B. & Tong, P. 2000 Turbulent thermal convection in a cell with ordered rough boundaries. J. Fluid Mech. 407, 57–84.CrossRefGoogle Scholar
Eckhardt, B., Grossmann, S. & Lohse, D. 2007a Fluxes and energy dissipation in thermal convection and shear flows. Europhys. Lett. 78, 24001.Google Scholar
Eckhardt, B., Grossmann, S. & Lohse, D. 2007b Torque scaling in turbulent Taylor–Couette flow between independently rotating cylinders. J. Fluid Mech. 581, 221–250.CrossRefGoogle Scholar
Fadlun, E. A., Verzicco, R., Orlandi, P. & Mohd-Yusof, J. 2000 Combined immersed-boundary finite-difference methods for three-dimensional complex flow simulations. J. Comput. Phys. 161, 35–60.Google Scholar
Fardin, M. A., Perge, C. & Taberlet, N. 2014 ‘The hydrogen atom of fluid dynamics’ – introduction to the Taylor–Couette flow for soft matter scientists. Soft Matt. 10, 3523–3535.CrossRefGoogle Scholar
van Gils, D. P. M., Huisman, S. G., Bruggert, G.-W., Sun, C. & Lohse, D. 2011 Torque scaling in turbulent Taylor–Couette flow with co- and counterrotating cylinders. Phys. Rev. Lett. 106, 024502.CrossRefGoogle ScholarPubMed
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.Google Scholar
Grossmann, S. & Lohse, D. 2001 Thermal convection for large Prandtl numbers. Phys. Rev. Lett. 86, 3316–3319.CrossRefGoogle ScholarPubMed
Grossmann, S. & Lohse, D. 2002 Prandtl and Rayleigh number dependence of the Reynolds number in turbulent thermal convection. Phys. Rev. E 66, 016301.Google ScholarPubMed
Grossmann, S. & Lohse, D. 2011 Multiple scaling in the ultimate regime of thermal convection. Phys. Fluids 23, 045108.Google Scholar
Grossmann, S. & Lohse, D. 2012 Logarithmic temperature profiles in the ultimate regime of thermal convection. Phys. Fluids 24, 125103.CrossRefGoogle Scholar
Grossmann, S., Lohse, D. & Sun, C. 2014 Velocity profiles in strongly turbulent Taylor–Couette flow. Phys. Fluids 26, 025114.Google Scholar
Grossmann, S., Lohse, D. & Sun, C. 2016 High Reynolds number Taylor–Couette flow. Annu. Rev. Fluid Mech. 48, 53–80.CrossRefGoogle Scholar
He, X., Funfschilling, D., Bodenschatz, E. & Ahlers, G. 2012a Heat transport by turbulent Rayleigh–Bénard convection for $Pr\simeq 0.8$ and $4\times 10^{11}\lesssim Ra\lesssim 2\times 10^{14}$ : ultimate-state transition for aspect ratio ${\it\Gamma}=1.00$ . New J. Phys. 14, 063030.Google Scholar
He, X., Funfschilling, D., Nobach, H., Bodenschatz, E. & Ahlers, G. 2012b Transition to the ultimate state of turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 108, 024502.CrossRefGoogle Scholar
Huisman, S. G., van Gils, D. P. M., Grossmann, S., Sun, C. & Lohse, D. 2012 Ultimate turbulent Taylor–Couette flow. Phys. Rev. Lett. 108, 024501.CrossRefGoogle ScholarPubMed
Huisman, S. G., Scharnowski, S., Cierpka, C., Kähler, C. J., Lohse, D. & Sun, C. 2013 Logarithmic boundary layers in strong Taylor–Couette turbulence. Phys. Rev. Lett. 110, 264501.CrossRefGoogle ScholarPubMed
Jimenez, J. 2004 Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36, 173–196.CrossRefGoogle Scholar
Kraichnan, R. H. 1962 Turbulent thermal convection at arbritrary Prandtl number. Phys. Fluids 5, 1374–1389.Google Scholar
Lathrop, D. P., Fineberg, J. & Swinney, H. L. 1992a Transition to shear-driven turbulence in Couette–Taylor flow. Phys. Rev. A 46, 6390–6405.Google Scholar
Lathrop, D. P., Fineberg, J. & Swinney, H. L. 1992b Turbulent flow between concentric rotating cylinders at large Reynolds number. Phys. Rev. Lett. 68, 1515–1518.CrossRefGoogle ScholarPubMed
Lewis, G. S. & Swinney, H. L. 1999 Velocity structure functions, scaling, and transitions in high-Reynolds-number Couette–Taylor flow. Phys. Rev. E 59, 5457–5467.Google Scholar
Marusic, I., Mckeon, B. J., Monkewitz, P. A., Nagib, H. M., Smits, A. J. & Sreenivasan, K. R. 2010 Wall-bounded turbulent flows at high Reynolds numbers: recent advances and key issues. Phys. Fluids. 22 (6), 065103.Google Scholar
Mittal, R. & Iaccarino, G. 2005 Immersed boundary methods. Annu. Rev. Fluid. Mech. 37, 239–261.Google Scholar
Nikuradse, J. 1933 Strömungsgesetze in rauhen Rohren. Forschungsheft Arb. Ing.-Wes. 361.Google Scholar
Ostilla, R., Stevens, R. J. A. M., Grossmann, S., Verzicco, R. & Lohse, D. 2013 Optimal Taylor–Couette flow: direct numerical simulations. J. Fluid Mech. 719, 14–46.Google Scholar
Ostilla-Mónico, R., van der Poel, E. P., Verzicco, R., Grossmann, S. & Lohse, D. 2014a Boundary layer dynamics at the transition between the classical and the ultimate regime of Taylor–Couette flow. Phys. Fluids 26, 015114.CrossRefGoogle Scholar
Ostilla-Mónico, R., van der Poel, E. P., Verzicco, R., Grossmann, S. & Lohse, D. 2014b Phase diagram of turbulent Taylor–Couette flow. J. Fluid Mech. 761, 1–26.Google Scholar
van der Poel, E. P., Ostilla-Mónico, R., Donners, J. & Verzicco, R. 2015a A pencil distributed code for simulating wall-bounded turbulent convection. Comput. Fluids 116, 10–16.CrossRefGoogle Scholar
van der Poel, E. P., Ostilla-Mónico, R., Verzicco, R., Grossmann, S. & Lohse, D. 2015b Logarithmic mean temperature profiles and their connection to plume emissions in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 115, 154501.Google Scholar
Pope, S. B. 2002 Wall flows. In Turbulent Flows, Cambridge Univerisity Press.Google Scholar
Qiu, X.-L., Xia, K.-Q. & Tong, P. 2005 Experimental study of velocity boundary layer near a rough conducting surface in turbulent natural convection. J. Turbul. 6, 1–13.Google Scholar
Roche, P.-E., Castaing, B., Chabaud, B. & Hébral, B. 2001 Observation of the $1/2$ power law in Rayleigh–Bénard convection. Phys. Rev. E 63, 045303(R).Google Scholar
Salort, J., Liot, O., Rusaouen, E., Seychelles, F., Tisserand, J. C., Creyssels, M., Castaing, B. & Chillà, F. 2014 Thermal boundary layer near roughnesses in turbulent Rayleigh–Bénard convection: flow structure and multistability. Phys. Fluids 26, 015112.Google Scholar
Shen, Y., Tong, P. & Xia, K.-Q. 1996 Turbulent convection over rough surfaces. Phys. Rev. Lett. 76, 908–911.Google Scholar
Smits, A. J., Mckeon, B. J. & Marusic, I. 2011 High-Reynolds number wall turbulence. Annu. Rev. Fluid. Mech. 43 (1), 353–375.Google Scholar
Stringano, G., Pascazio, G. & Verzicco, R. 2006 Turbulent thermal convection over grooved plates. J. Fluid Mech. 557, 307–336.CrossRefGoogle Scholar
Tisserand, J. C., Creyssels, M., Gasteuil, Y., Pabiou, H., Gibert, M., Castaing, B. & Chillà, F. 2011 Comparison between rough and smooth plates within the same Rayleigh–Bénard cell. Phys. Fluids 23, 015105.CrossRefGoogle Scholar
Verzicco, R. & Orlandi, P. 1996 Afinite-difference scheme for three-dimensional incompressible flows in cylindrical coordinates. J. Comput. Phys. 123, 402–413.Google Scholar
Wei, P., Chan, T.-S., Ni, R., Zhao, X.-Z. & Xia, K.-Q. 2014 Heat transport properties of plates with smooth and rough surfaces in turbulent thermal convection. J. Fluid Mech. 740, 28–46.CrossRefGoogle Scholar