Article contents
Extender sets and multidimensional subshifts
Published online by Cambridge University Press: 02 October 2014
Abstract
In this paper, we consider a 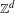 $\mathbb{Z}^{d}$ extension of the well known fact that subshifts with only finitely many follower sets are sofic. As in Kass and Madden [A sufficient condition for non-soficness of higher-dimensional subshifts. Proc. Amer. Math. Soc.141 (2013), 3803–3816], we adopt a natural
$\mathbb{Z}^{d}$ extension of the well known fact that subshifts with only finitely many follower sets are sofic. As in Kass and Madden [A sufficient condition for non-soficness of higher-dimensional subshifts. Proc. Amer. Math. Soc.141 (2013), 3803–3816], we adopt a natural 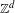 $\mathbb{Z}^{d}$ analogue of a follower set called an extender set. The extender set of a finite word
$\mathbb{Z}^{d}$ analogue of a follower set called an extender set. The extender set of a finite word 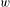 $w$ in a
$w$ in a 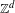 $\mathbb{Z}^{d}$ subshift
$\mathbb{Z}^{d}$ subshift 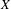 $X$ is the set of all configurations of symbols on the rest of
$X$ is the set of all configurations of symbols on the rest of 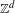 $\mathbb{Z}^{d}$ which form a point of
$\mathbb{Z}^{d}$ which form a point of 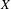 $X$ when concatenated with
$X$ when concatenated with 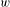 $w$. As our main result, we show that for any
$w$. As our main result, we show that for any 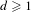 $d\geq 1$ and any
$d\geq 1$ and any 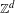 $\mathbb{Z}^{d}$ subshift
$\mathbb{Z}^{d}$ subshift 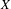 $X$, if there exists
$X$, if there exists  $n$ so that the number of extender sets of words on a
$n$ so that the number of extender sets of words on a 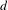 $d$-dimensional hypercube of side length
$d$-dimensional hypercube of side length  $n$ is less than or equal to
$n$ is less than or equal to  $n$, then
$n$, then 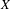 $X$ is sofic. We also give an example of a non-sofic system for which this number of extender sets is
$X$ is sofic. We also give an example of a non-sofic system for which this number of extender sets is 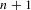 $n+1$ for every
$n+1$ for every  $n$. We prove this theorem in two parts. First we show that if the number of extender sets of words on a
$n$. We prove this theorem in two parts. First we show that if the number of extender sets of words on a 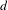 $d$-dimensional hypercube of side length
$d$-dimensional hypercube of side length  $n$ is less than or equal to
$n$ is less than or equal to  $n$ for some
$n$ for some  $n$, then there is a uniform bound on the number of extender sets for words on any sufficiently large rectangular prism; to our knowledge, this result is new even for
$n$, then there is a uniform bound on the number of extender sets for words on any sufficiently large rectangular prism; to our knowledge, this result is new even for 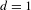 $d=1$. We then show that such a uniform bound implies soficity. Our main result is reminiscent of the classical Morse–Hedlund theorem, which says that if
$d=1$. We then show that such a uniform bound implies soficity. Our main result is reminiscent of the classical Morse–Hedlund theorem, which says that if  $X$ is a
$X$ is a  $\mathbb{Z}$ subshift and there exists an
$\mathbb{Z}$ subshift and there exists an  $n$ such that the number of words of length
$n$ such that the number of words of length  $n$ is less than or equal to
$n$ is less than or equal to  $n$, then
$n$, then 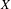 $X$ consists entirely of periodic points. However, most proofs of that result use the fact that the number of words of length
$X$ consists entirely of periodic points. However, most proofs of that result use the fact that the number of words of length  $n$ in a
$n$ in a  $\mathbb{Z}$ subshift is non-decreasing in
$\mathbb{Z}$ subshift is non-decreasing in  $n$, and we present an example (due to Martin Delacourt) which shows that this monotonicity does not hold for numbers of extender sets (or follower sets) of words of length
$n$, and we present an example (due to Martin Delacourt) which shows that this monotonicity does not hold for numbers of extender sets (or follower sets) of words of length  $n$.
$n$.
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press, 2014
References
- 5
- Cited by




