Hostname: page-component-8448b6f56d-qsmjn Total loading time: 0 Render date: 2024-04-23T22:38:47.577Z Has data issue: false hasContentIssue false
  • English
  • Français

Travelling wave states in pipe flow

Published online by Cambridge University Press:  22 February 2016

Ozge Ozcakir ,
Saleh Tanveer ,
Philip Hall  and
Edward A. Overman II
Ozge Ozcakir
Affiliation:
School of Mathematical Sciences, Monash University, Clayton, VIC 3800, Australia
Saleh Tanveer
Affiliation:
Department of Mathematics, The Ohio State University, Columbus, OH 43210, USA
Philip Hall*
Affiliation:
School of Mathematical Sciences, Monash University, Clayton, VIC 3800, Australia
Edward A. Overman II
Affiliation:
Department of Mathematics, The Ohio State University, Columbus, OH 43210, USA
*
†Email address for correspondence: philhall@ic.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we have found two new nonlinear travelling wave solutions in pipe flows. We investigate possible asymptotic structures at large Reynolds number 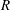$R$ when wavenumber is independent of 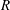$R$ and identify numerically calculated solutions as finite 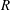$R$ realizations of a nonlinear viscous core (NVC) state that collapses towards the pipe centre with increasing $R$ at a rate 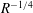$R^{-1/4}$. We also identify previous numerically calculated states as finite 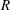$R$ realizations of a vortex wave interacting (VWI) state with an asymptotic structure similar to the ones in channel flows studied earlier by Hall & Sherwin (J. Fluid Mech., vol. 661, 2010, pp. 178–205). In addition, asymptotics suggests the possibility of a VWI state that collapses towards the pipe centre like 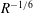$R^{-1/6}$, though this remains to be confirmed numerically.

JFM classification

Instability: Instability Instability: Nonlinear instability Instability: Transition to turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 791 , 25 March 2016 , pp. 284 - 328
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Batchelor, G. K. & Gill, A. E. 1962 Analysis of the stability of axisymmetric jets. J. Fluid Mech. 14 (4), 529–551.CrossRefGoogle Scholar
Blackburn, H. M., Hall, P. & Sherwin, S. J. 2013 Lower branch equilibria in Couette flow: the emergence of canonical states for arbitrary shear flows. J. Fluid Mech. 726, R2.CrossRefGoogle Scholar
Deguchi, K. & Hall, P. 2014a Free-stream coherent structures in parallel boundary-layer flows. J. Fluid Mech. 752, 602–625.CrossRefGoogle Scholar
Deguchi, K. & Hall, P. 2014b Canonical exact coherent structures embedded in high Reynolds number flows. Phil. Trans. R. Soc. Lond. A 372, 20130352.Google ScholarPubMed
Deguchi, K. & Walton, A. G. 2013 A swirling spiral wave solution in pipe flow. J. Fluid Mech. 737 (R2), 1–12.CrossRefGoogle Scholar
Faisst, H. & Eckhardt, B. 2003 Traveling waves in pipe flow. Phys. Rev. Lett. 91, 224502.Google Scholar
Fitzerald, R. 2004 New experiments set the scale for the onset for the onset of turbulence in pipe flow. Phys. Today 57 (2), 21–24.Google Scholar
Gibson, J. F., Halcrow, J. & Cvitanovic, P. 2009 Equilibrium and travelling-wave solutions of plane Couette flow. J. Fluid Mech. 638, 243–266.Google Scholar
Hall, P. & Sherwin, S. 2010 Streamwise vortices in shear flows: harbingers of transition and the skeleton of coherent structures. J. Fluid Mech. 661, 178–205.Google Scholar
Hall, P. & Smith, F. 1991 On strongly nonlinear vortex/wave interactions in boundary layer transition. J. Fluid Mech. 227, 641–666.CrossRefGoogle Scholar
Hof, B., van Doorne, C., Westerweel, J., Nieuwstadt, F., Faisst, H., Eckhardt, B., Wedin, H., Kerswell, R. & Waleffe, F. 2004 Experimental observation of nonlinear traveling waves in the turbulent pipe flow. Science 305 (5690), 1594–1598.Google Scholar
Kerswell, R. & Tutty, O. 2007 Recurrence of traveling waves in transitional pipe flow. J. Fluid Mech. 584, 69–102.CrossRefGoogle Scholar
Pringle, C. C. T., Duguet, Y. & Kerswell, R. R. 2009 Highly symmetric travelling waves in pipe flow. Phil. Trans. R. Soc. Lond. A 367 (1888), 457–472.Google ScholarPubMed
Pringle, C. C. T. & Kerswell, R. R. 2007 Asymmetric, helical and mirror-symmetric travelling waves in pipe flow. Phys. Rev. Lett. 99, 074502.CrossRefGoogle ScholarPubMed
Nagata, M. 1990 Three dimensional finite-amplitude solutions in plane Coutte flow: bifurcation from infinity. J. Fluid Mech. 217, 519–527.CrossRefGoogle Scholar
Ozcakir, O.2014 Vortex–wave solutions of Navier–Stokes equations in a cylindrical pipe. PhD thesis, The Ohio State University.Google Scholar
Schneider, T. & Eckhardt, B. 2009 Edge states intermediate between laminar and turbulent dynamics in pipe flow. Phil. Trans. R. Soc. Lond. A 367, 577–587.Google ScholarPubMed
Smith, F. T. & Bodonyi, R. J. 1982 Amplitude-dependent neutral modes in the Hagen–Poiseille flow through a circular pipe. Proc. R. Soc. Lond. A 384, 463–489.Google Scholar
Viswanath, D. 2007 Recurrent motions within plane Couette turbulence. J. Fluid Mech. 580, 339–358.CrossRefGoogle Scholar
Viswanath, D. 2009 Critical layer in pipe flow at high Reynolds number. Phil. Trans. R. Soc. Lond. A 580, 561–576.Google Scholar
Viswanath, D. & Cvitanovic, P. 2009 Stable manifolds and the transition to turbulence in pipe flow. J. Fluid Mech. 627, 215–233.Google Scholar
Waleffe, F. 1995 Hydrodynamic stability and turbulence: beyond transients to a self-sustaining process. Stud. Appl. Maths 95 (3), 319–343.CrossRefGoogle Scholar
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9 (4), 883–900.Google Scholar
Waleffe, F. 1998 Three dimensional coherent states in plane shear flows. Phys. Rev. Lett. 81 (19), 4140–4143.CrossRefGoogle Scholar
Waleffe, F. 2001 Exact coherent structures in channel flow. J. Fluid Mech. 435, 93–102.CrossRefGoogle Scholar
Waleffe, F. 2003 Homotopy of exact coherent structures in plane shear flows. Phys. Fluids 15 (6), 1517–1534.CrossRefGoogle Scholar
Wang, J., Gibson, J. & Waleffe, F. 2007 Lower branch coherent states in shear flows: transition and control. Phys. Rev. Lett. 98 (20), 204501.CrossRefGoogle ScholarPubMed
Wedin, H. & Kerswell, R. 2004 Exact coherent structures in pipe flow: travelling wave solutions. J. Fluid Mech. 508, 333–371.CrossRefGoogle Scholar