Hostname: page-component-8448b6f56d-42gr6 Total loading time: 0 Render date: 2024-04-25T04:56:55.828Z Has data issue: false hasContentIssue false
  • English
  • Français

METRIC RESULTS ON THE DISCREPANCY OF SEQUENCES 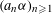$(a_{n}{\it\alpha})_{n\geqslant 1}$ MODULO ONE FOR INTEGER SEQUENCES 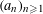$(a_{n})_{n\geqslant 1}$ OF POLYNOMIAL GROWTH

Part of: Probabilistic theory: distribution modulo $1$; metric theory of algorithms Exponential sums and character sums

Published online by Cambridge University Press:  05 February 2016

Christoph Aistleitner  and
Gerhard Larcher
Christoph Aistleitner
Affiliation:
Institute of Financial Mathematics and Applied Number Theory, University Linz, Altenbergerstrasse 69, 4040 Linz, Austria email aistleitner@math.tugraz.at
Gerhard Larcher
Affiliation:
Institute of Financial Mathematics and Applied Number Theory, University Linz, Altenbergerstrasse 69, 4040 Linz, Austria email gerhard.larcher@jku.at
Get access

Abstract

An important result of Weyl states that for every sequence 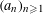$(a_{n})_{n\geqslant 1}$ of distinct positive integers the sequence of fractional parts of 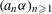$(a_{n}{\it\alpha})_{n\geqslant 1}$ is uniformly distributed modulo one for almost all ${\it\alpha}$. However, in general it is a very hard problem to calculate the precise order of convergence of the discrepancy of 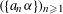$(\{a_{n}{\it\alpha}\})_{n\geqslant 1}$ for almost all ${\it\alpha}$. In particular, it is very difficult to give sharp lower bounds for the speed of convergence. Until now this was only carried out for lacunary sequences 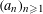$(a_{n})_{n\geqslant 1}$ and for some special cases such as the Kronecker sequence 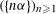$(\{n{\it\alpha}\})_{n\geqslant 1}$ or the sequence 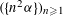$(\{n^{2}{\it\alpha}\})_{n\geqslant 1}$. In the present paper we answer the question for a large class of sequences 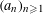$(a_{n})_{n\geqslant 1}$ including as a special case all polynomials 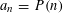$a_{n}=P(n)$ with 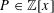$P\in \mathbb{Z}[x]$ of degree at least 2.

MSC classification

Primary: 11K38: Irregularities of distribution, discrepancy 11K55: Metric theory of other algorithms and expansions; measure and Hausdorff dimension 11L07: Estimates on exponential sums
Type
Research Article
Information
Mathematika , Volume 62 , Issue 2 , 2016 , pp. 478 - 491
Copyright
Copyright © University College London 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aistleitner, C., Berkes, I. and Seip, K., GCD sums from Poisson integrals and systems of dilated functions. J. Eur. Math. Soc. 17(6) 2015, 1517–1546.CrossRefGoogle Scholar
Aistleitner, C., Berkes, I., Seip, K. and Weber, M., Convergence of series of dilated functions and spectral norms of GCD matrices. Acta Arith. 168(3) 2015, 221–246.CrossRefGoogle Scholar
Aistleitner, C., Hofer, R. and Larcher, G., On parametric Thue–Morse sequences and lacunary trigonometric products. Preprint, 2015, arXiv:1502.06738.Google Scholar
Baker, R. C., Metric number theory and the large sieve. J. Lond. Math. Soc. (2) 24(1) 1981, 34–40.CrossRefGoogle Scholar
Berkes, I. and Philipp, W., The size of trigonometric and Walsh series and uniform distribution mod 1. J. Lond. Math. Soc. (2) 50(3) 1994, 454–464.CrossRefGoogle Scholar
Drmota, M. and Tichy, R. F., Sequences, Discrepancies and Applications (Lecture Notes in Mathematics 1651 ), Springer (Berlin, 1997).CrossRefGoogle Scholar
Dyer, T. and Harman, G., Sums involving common divisors. J. Lond. Math. Soc. (2) 34(1) 1986, 1–11.CrossRefGoogle Scholar
Fiedler, H., Jurkat, W. and Körner, O., Asymptotic expansions of finite theta series. Acta Arith. 32 1977, 129–146.CrossRefGoogle Scholar
Fouvry, E. and Mauduit, C., Sommes des chiffres et nombres presque premiers. Math. Ann. 305(3) 1996, 571–599.CrossRefGoogle Scholar
Fukuyama, K., The law of the iterated logarithm for discrepancies of {𝜃 n x}. Acta Math. Hungar. 118(1–2) 2008, 155–170.CrossRefGoogle Scholar
Hardy, G. H. and Wright, E. M., An Introduction to the Theory of Numbers, 5th edn., Oxford Science (1979).Google Scholar
Hilberdink, T., An arithmetical mapping and applications to Ω-results for the Riemann zeta function. Acta Arith. 139(4) 2009, 341–367.CrossRefGoogle Scholar
Khintchine, A., Einige Sätze über Kettenbrüche, mit Anwendungen auf die Theorie der Diophantischen Approximationen. Math. Ann. 92 1924, 115–125.CrossRefGoogle Scholar
Kuipers, L. and Niederreiter, H., Uniform Distribution of Sequences, Wiley (New York–London–Sydney, 1974).Google Scholar
Larcher, G., Probabilistic Diophantine approximation and the distribution of Halton–Kronecker sequences. J. Complexity 29 2013, 397–423.CrossRefGoogle Scholar
LeVeque, W. J., On the frequency of small fractional parts in certain real sequences III. J. reine angew. Math. 202 1959, 215–220.CrossRefGoogle Scholar
Mahler, K., Zur approximation algebraischer Zahlen II. Math. Ann. 108 1933, 37–55.CrossRefGoogle Scholar
Philipp, W., Limit theorems for lacunary series and uniform distribution mod 1. Acta Arith. 26(3) 1974–1975, 241–251.CrossRefGoogle Scholar
Weyl, H., Über die Gleichverteilung von Zahlen modulo Eins. Math. Ann. 77 1916, 313–352.CrossRefGoogle Scholar
Zygmund, A., Trigonometric Series, Vols. I, II (Cambridge Mathematical Library), Cambridge University Press (Cambridge, 1988) . Reprint of the 1979 edition.Google Scholar